Предмет: Математика,
автор: yomadip552
Докажите неравенство
Приложения:
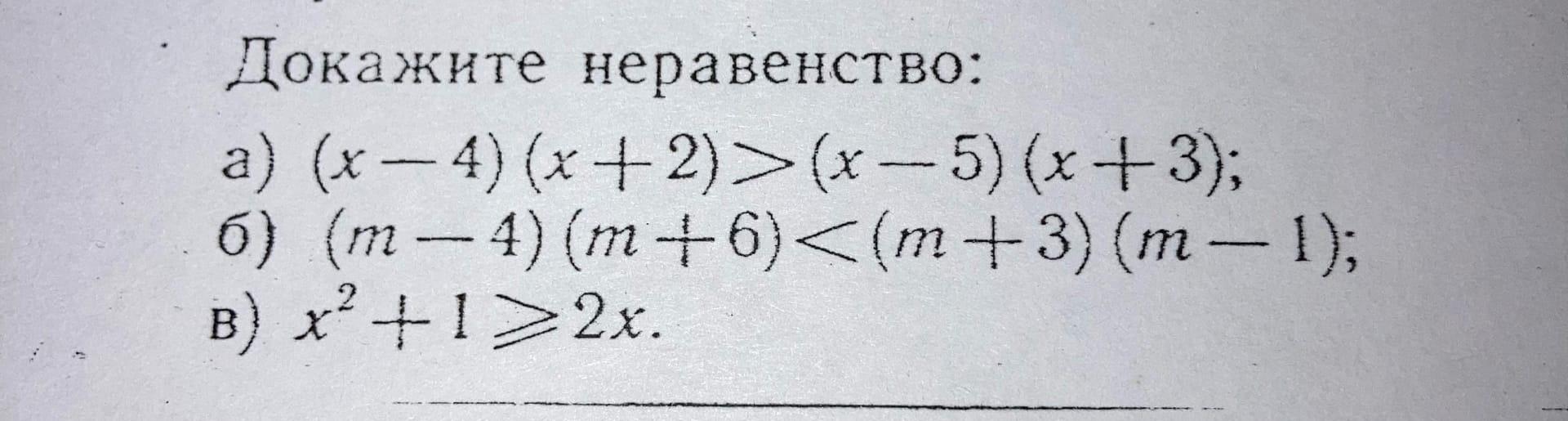
yomadip552:
ну как там?
Ответы
Автор ответа:
0
а) (х - 4)(х + 2) > (х - 5)(х + 3)
х² - 4х +2х - 8 > х² - 5х + 3х - 15
х² - 2х - 8 > х² - 2х - 15
Сократим в обеих частях х² и -2х
-8 > -15 - неравенство верное.
б) (m - 4)(m + 6) < (m + 3)(m - 1)
m² - 4m + 6m - 24 < m² + 3m - m - 3
m² + 2m - 24 < m² + 2m - 3
Сократим в обеих частях m² и 2m
-24 < -3 - неравенство верное.
в) х² + 1 ≥ 2х
Прибавим в левой части неравенства 2х и вычтем 2х:
х² + 1 + 2х - 2х ≥ 2х
Сократим в обеих частях 2х:
(х² - 2х + 1) + 2х ≥ 2х
(х - 1)² ≥ 0 - верное равенство, поскольку квадрат выражения всегда больше 0 или равен 0
Похожие вопросы
Предмет: Русский язык,
автор: jtpa
Предмет: Русский язык,
автор: Oleshkas
Предмет: Русский язык,
автор: никитос09052006
Предмет: Українська мова,
автор: Irenka40