Предмет: Геометрия,
автор: antoncreepp1
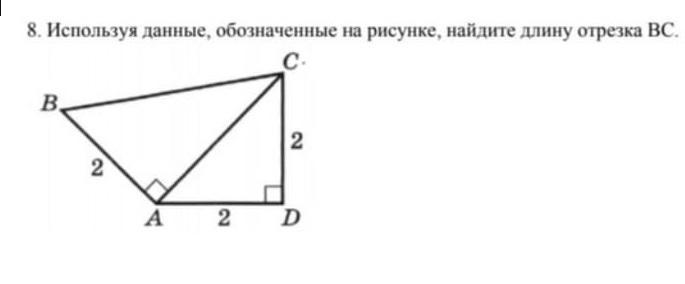
используя данные обозначенные на рисунке найдите длину отрезка BC
Приложения:
Ответы
Автор ответа:
2
Так как треугольник ACD — прямоугольный, то гипотенузу AC — можно найти по двум катетам (AD & CD) по теореме Пифагора:
В треугольнике ACD — отрезок AC — гипотенуза, но в треугольнике BAC — катет.
Так как нам известны катеты треугольника BAC, то теорема та жа:
Вывод: BC = 3.5.
Аноним:
Да, я ошиблась, извините.
Похожие вопросы
Предмет: Русский язык,
автор: yadenkoff
Предмет: Русский язык,
автор: melan7575
Предмет: Українська мова,
автор: настюха104
Предмет: Русский язык,
автор: гулжан9
Предмет: Математика,
автор: Анонимный112