Предмет: Геометрия,
автор: nirvanaEC
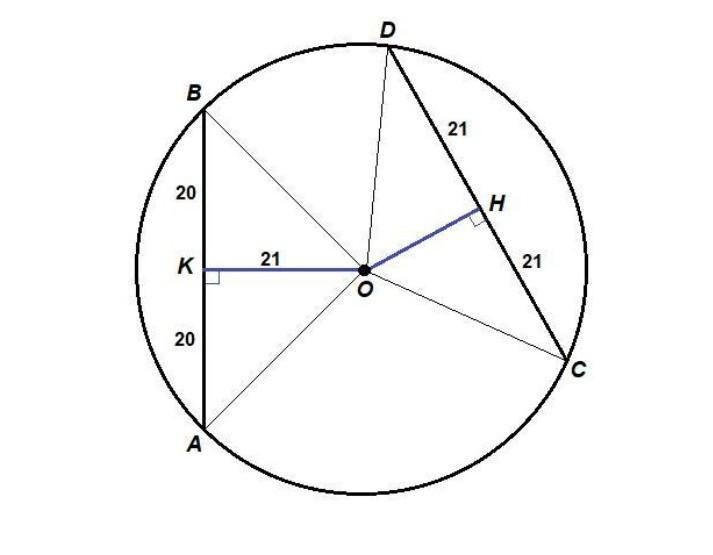
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=40, CD=42, а расстояние от центра окружности до хорды AB равно 21
Ответы
Автор ответа:
2
Ответ:
20
Объяснение:
Соединим центр окружности с концами хорд.
= = OC = OD как радиусы.
Проведем OK.LAB и и OH. LCD, OK = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ДОАВ равнобедренный, значит OK - высота и медиана.
AK = KB = 1/2AB = 1/2 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
= /(AK2 + KO2) = v(202 + 212) = v(400
+ 441) = +/841 = 29 CO = AO = 29
ACOD равнобедренный, значит ОН - высота и медиана,
CH = HD = 1/2CD = 1/2 42 = 21 Из прямоугольного треугольника СОН по теореме Пифагора:
ОН = v(CO2 - CH?) = -/(292 - 212) = v(841 - 441) = v400 = 20
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Ruslan00077722
Предмет: Русский язык,
автор: ЗЕНИТиЛОКО
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: alika38