Найти общее решение линейного дифференциального уравнения второго порядка.
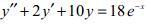
Ответы
Ответ:
или так
Объяснение:
Найти общее решение линейного дифференциального уравнения второго порядка.
y'' + 2y' + 10y = 18e⁻ˣ
Для решения неоднородного диф. уравнения применяем метод метод неопределенных коэффициентов.
Общее решение y(x) линейного неоднородного дифференциального уравнения равно сумме общего решения y (x) одн соответствующего
однородного уравнения и частного решения y (x) част исходного неоднородного уравнения.
y(x) = y(х)одн + y(х)част
Найдем решение однородного уравнения
y'' + 2y' + 10y = 0
Составим и решим характеристическое уравнение:
k² + 2k + 10 = 0
k₁ = -1 - 3i k₂ = -1 + 3i
Запишем общее решение однородного уравнения
(для корней вида k = a ± b·i общее решение
y = С₁·eᵃˣ·cos(bx) + C₂·eᵃˣ·sin(bx))
y(х)одн = С₁·e⁻ˣ·cos(3x) + C₂·e⁻ˣ·sin(3x)
Частное решение ищем в виде
s=0 если α+βi не корень характеристического уравнения
В нашем случае α+βi = -1 следовательно s=0
Поэтому частное решение ищем в виде
у = А·e⁻ˣ
Вычисляем производные
у' = -А·e⁻ˣ
у" = А·e⁻ˣ
Подставляем в исходное уравнение
y'' + 2y' + 10y = 18e⁻ˣ
А·e⁻ˣ' - 2А·e⁻ˣ + 10А·e⁻ˣ = 18e⁻ˣ
9А·e⁻ˣ = 18e⁻ˣ
A = 2
Частное решение
y(х)част = 2e⁻ˣ
Запишем общее решение
y(x) = y(х)одн + y(х)част = С₁·e⁻ˣ·cos(3x) + C₂·e⁻ˣ·sin(3x) + 2e⁻ˣ =
= (С₁·cos(3x) + C₂·sin(3x) + 2)·e⁻ˣ