Предмет: Геометрия,
автор: Аноним
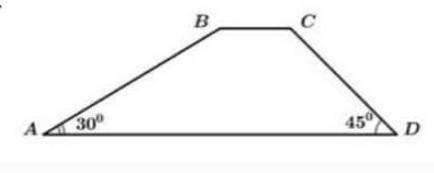
В трапеции ABCD, показанной на рисунке AD II BC, BC- 1см, AB = 2 см, BAD = 30° CDA = 45° найти площадь Трапеций ABCD.
Приложения:
Ответы
Автор ответа:
1
Ответ:
(3+√3)/2 см²
Объяснение:
Проведем высоты ВН и СК. КН=ВС=1 см.
ΔАВН - прямоугольный, ВН=1/2 АВ по свойству катета, лежащего против угла 30°; ВН=СК=1 см.
По теореме Пифагора АН=√(АВ²-ВН²)=√(4-1)=√3 см.
Δ СКD - прямоугольный, ∠СКD=90-45=45° т.к. сумма острых углов прямоугольного треугольника 90°, значит ΔСКD - равнобедренный и КD=СК=1 см.
AD=1+1+√3=2+√3 см
S=(ВС+AD):2*BH=(1+2+√3):2*1=(3+√3)/2 см²
ffeefdf:
пеппер пожалуйста помогите с геометрией
Похожие вопросы
Предмет: Русский язык,
автор: айханкрутой2
Предмет: Українська мова,
автор: slavik54
Предмет: Українська література,
автор: yatsyshina86
Предмет: Биология,
автор: elizaveta196