Question

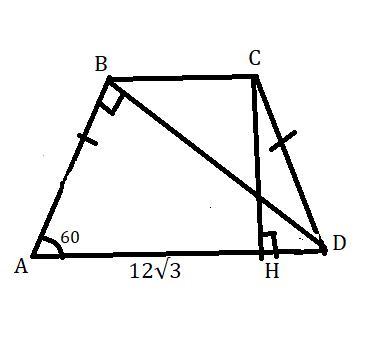
СРОЧНО СРОЧНО СРОЧНО !в равнобедренной трапеции диагональ перпендикулярна боковой стороне. найти площадь трапеции если большее основание равно 12 √ 3 , а один из углов трапеции равен 60° . ВСЁ РАСПИСОВАТЬ.

Answer 1

Ответ:SABCD=81√3см²

Объяснение:

SABCD=$\frac{1}{2} (AD+BC)*CH$

1.ΔADB(∠B=90°):

∠ADB=90-∠BAD=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)

AB=1/2AD=$\frac{1*12\sqrt{3} }{2} =6\sqrt{3}$см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)

2.Трапеция ABCD:

AB=CD=6√3см(В равнобокой трапеции боковые стороны равны)

∠A=∠D=60(В равнобокой трапеции  углы при основаниях равны)

3.ΔDCH(∠H=90°):

∠DCH=90-∠CDH=90-60=30°(Сумма острых углов прямоугольного треугольника равна 90)

HD=1/2CD=6√3/2=3√3см(Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.)

sinCDH=CH/CD

CH=sinCDH*CD=sin60*6√3=$\frac{\sqrt{3} *6\sqrt{3} }{2} =\frac{6*3}{2} =9$см

4.Трапеция ABCD:

$HD=\frac{AD-BC}{2}$(Ссвойство равнобедренной трапеции)

AD-BC=2HD

-BC=-AD+2HD

BC=AD-2HD=12√3-2*3√3=12√3-6√3=6√3см

SABCD=$\frac{1}{2} (12\sqrt{3} +6\sqrt{3} )*9=\frac{18\sqrt{3} }{2} *9=9\sqrt{3} *9=81\sqrt{3}$см²