Предмет: Математика,
автор: dimakoles2004
Помогите решить тригонометрические неравинства
Приложения:
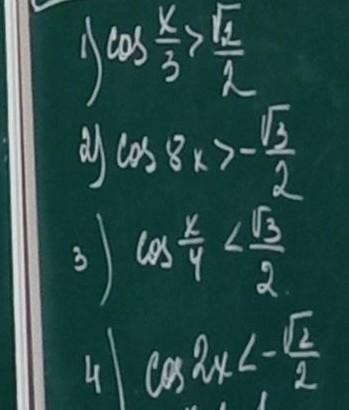
Ответы
Автор ответа:
2
Ответ:
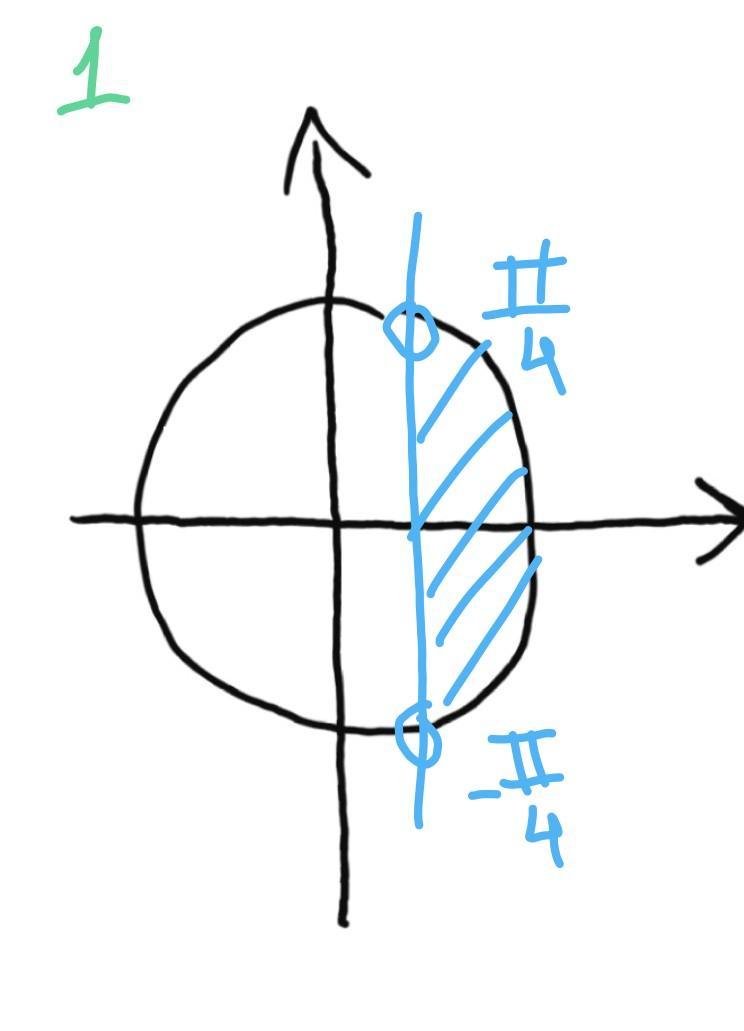
1.
рисунок1
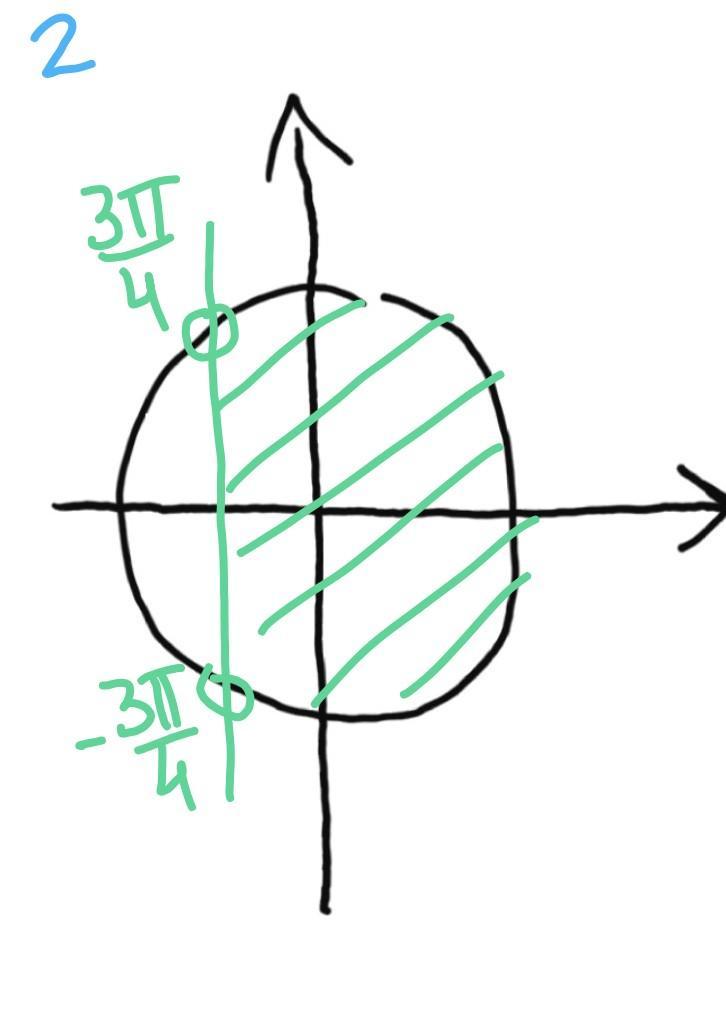
2.
рисунок 2
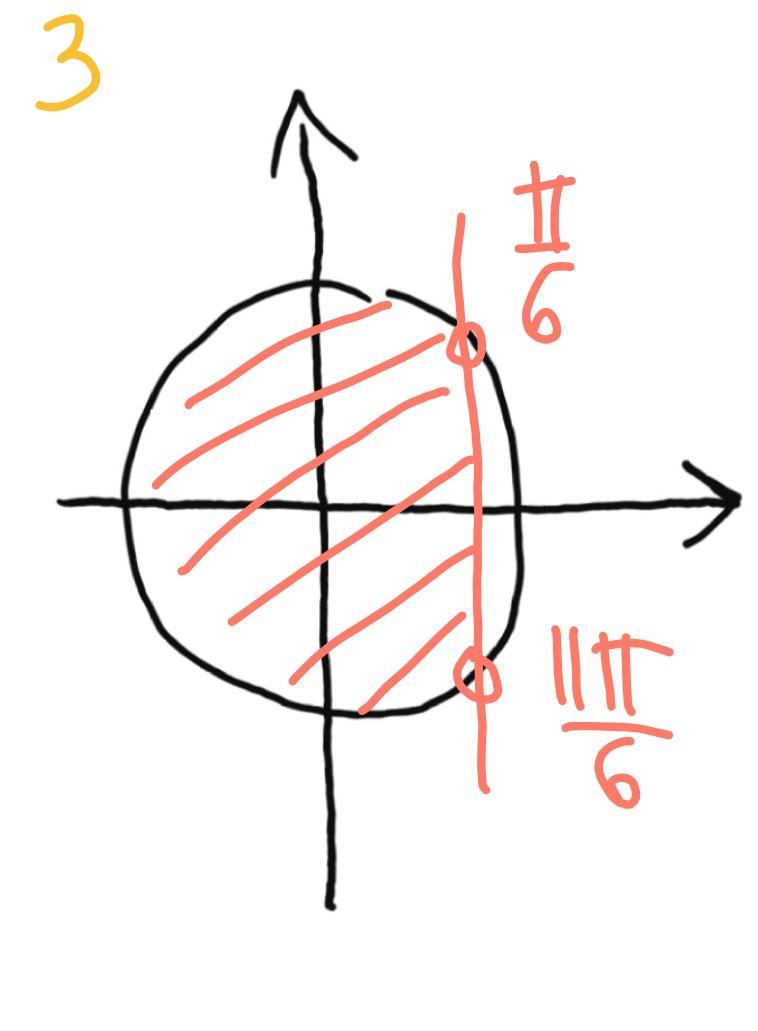
3.
рисунок 3
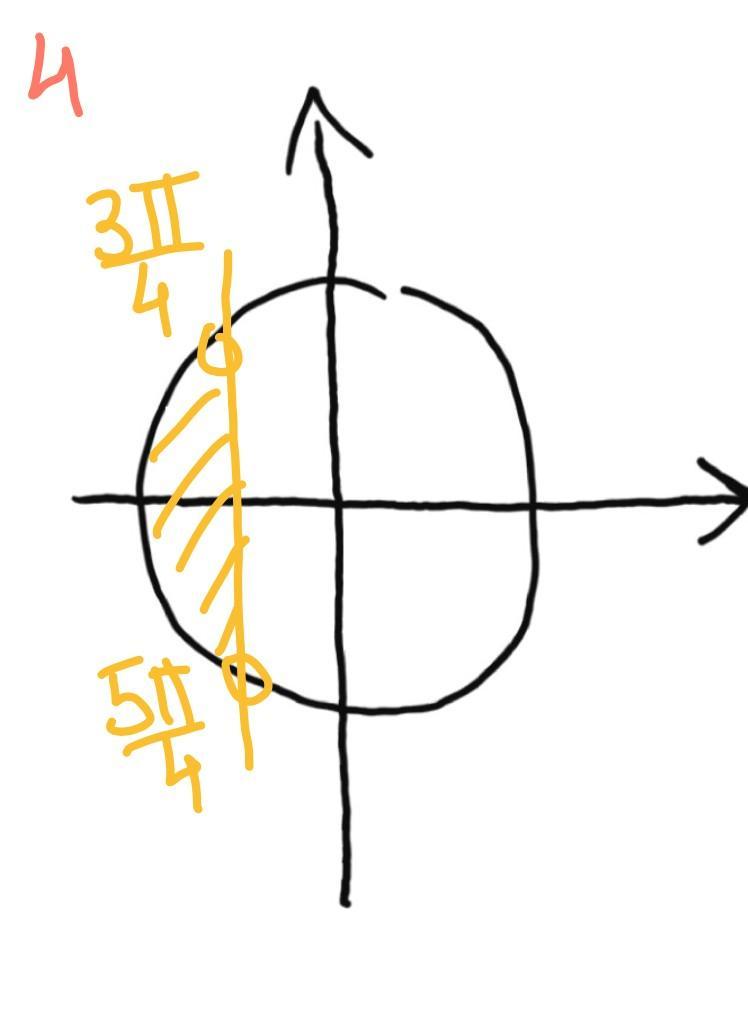
4.
рисунок 4
везде n принадлежит Z.
Приложения:
fiufjf0:
мне помогите пожалуйста умоляю надо
пожалуйста помогите пожалуйста умоляю
спс
помогите пожалуйста
Похожие вопросы
Предмет: Українська мова,
автор: 0966131335
Предмет: Русский язык,
автор: патюлька1
Предмет: Русский язык,
автор: carinakosenko
Предмет: Математика,
автор: pogorelovschij
Предмет: Литература,
автор: akasuhrob