Предмет: Алгебра,
автор: xgamerxpowerp9qy5j
Вычислить следующие интегралы методом подстановки
Приложения:
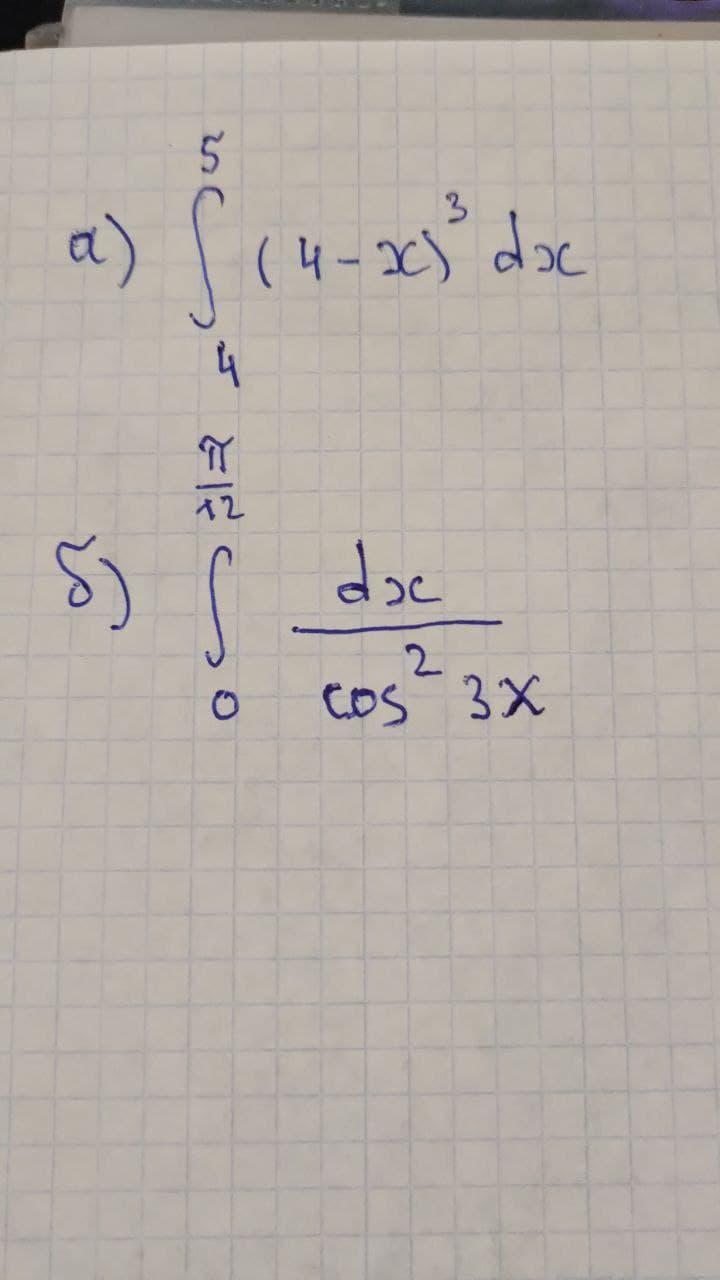
Ответы
Автор ответа:
1
Ответ:
1
2
Похожие вопросы
Предмет: Русский язык,
автор: gorbunova8787
Предмет: Окружающий мир,
автор: lola322
Предмет: Русский язык,
автор: килер3
Предмет: Литература,
автор: alyaermolaeva
Предмет: Русский язык,
автор: элина336