Question

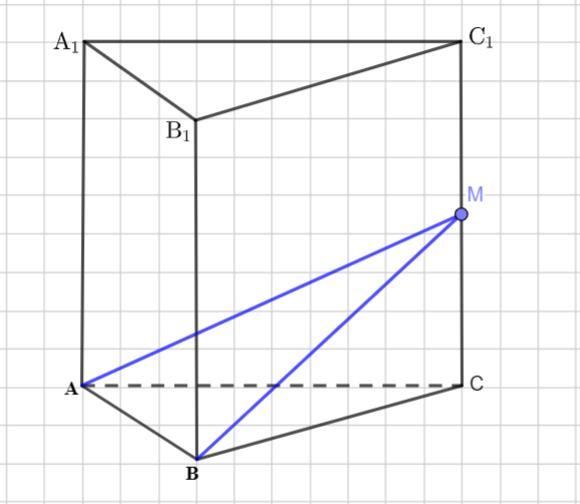
об'єм прямої трикутної призми АВСА¹В¹С¹ дорівнює 48см³ точка М середина ребра СС¹ обчисліть об'єм піраміди МАВС​

Answer 1

Ответ:

8 см³.

Объяснение:

Дана прямая треугольная призма $ABAA_{1} B_{1} C_{1}$

V= 48 cм³.

Объём призмы равен произведению площади основания на высоту .

$V=S(ABC)\cdot H;\\V=S(ABC)\cdot C C_{1}$

Значит,

$S(ABC)\cdot C C_{1}=48$

Объем пирамиды определяется  по формуле

$V=\dfrac{1}{3} \cdot S\cdot H,$

где S- площадь основания, H- высота пирамиды.

Основанием пирамиды МАВС является треугольник АВС.

Отрезок СМ - высота пирамиды. Так как точка М -середина бокового ребра $CC_{1}$, то $CM=\dfrac{1}{2} CC_{1}$

Тогда найдем объем пирамиды

$V=\dfrac{1}{3} \cdot S(ABC) \cdot CM;\\\\V=\dfrac{1}{3} \cdot S(ABC) \cdot \dfrac{1}{2} CC_{1} ;\\\\V=\dfrac{1}{6} \cdot S(ABC) \cdot CC_{1} ;\\\\V=\dfrac{1}{6} \cdot48=8$

Значит, объем пирамиды МАВС равен 8 см³