Предмет: Алгебра,
автор: Аноним
Решите умоляю!!! Сдавать через 30 минут!!!
Приложения:
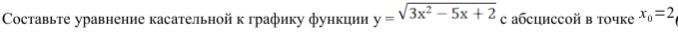
Ответы
Автор ответа:
1
Ответ:
y=1,75x-1,5
Объяснение:
Уравнение касательной в точке x0 имеет вид
. f'(x0) - это производная исходной функции в точке х0, f(x) - сама функция в точке, f(x)=√3x^2-5x+2, x0=2
Для начала найдем производную функцию, как производную от сложной функции, т.е. сначала находим производную внешней функции, а потом умножаем ее на производную внутренней, внешняя функция квадратный корень. Производная квадратного корня равна дробь делить на 2 таких корня. Внутренняя функция - квадратный трехчлен. Производная суммы равна сумме производных, поэтому отдельно находим производную квадратного трехчлена как производные степенных функций получим
найдем производную в точке 2, для этого вместо икс подставим 2
. Подставим в формулу
Похожие вопросы
Предмет: Русский язык,
автор: katyaibadova
Предмет: Другие предметы,
автор: 64777viva
Предмет: Русский язык,
автор: 79173992216
Предмет: Литература,
автор: юся351
Предмет: Алгебра,
автор: марка24