Предмет: Алгебра,
автор: pio68
50 баллов
разность квадратов двух чисел равна 105, а сумма этих чисел 15. найдите эти числа
Ответы
Автор ответа:
0
Ответ:
Проверка:
Приложения:
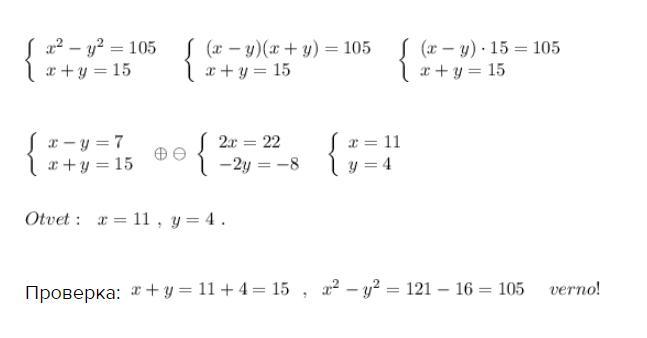
pio68:
не можешь ли написать? выдаёт баг и ничего не понятно, просто код
сейчас
??
а показало
спасибо
а как получилось 7?
а я понял
Похожие вопросы
Предмет: Українська мова,
автор: 19792511ania
Предмет: Русский язык,
автор: anstrelkova93
Предмет: Окружающий мир,
автор: муся46
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: aleksaboo