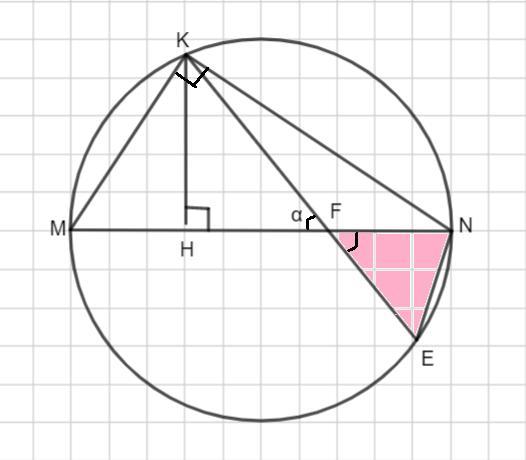
На окружности с диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает диаметр MN в точке F под углом, равным arccos4/5
а)Докажите,что KF:FE=125:29.
б) Найдите площадь треугольника KEN.
Ответы
Ответ:
Площадь треугольника Δ KEN равна 8,7 кв. ед.
Пошаговое объяснение:
На рисунке Δ MKN - прямоугольный, так как ∠ MKN опирается на диаметр MN .
По условию MN= 34 ед. , KH = 15 ед., α=arccos 4/5.
Угол α - острый.
KH - высота прямоугольного треугольника Δ MKN .
Высота прямоугольного треугольника, проведенная к гипотенузе есть среднее пропорциональное между отрезками, на которые делится гипотенуза основанием высоты.
Пусть MH = x. Тогда HN= 34-x
MH= 9 ед. , HN= 34-9=25 ед.
Если α=arccos 4/5, то cos α =4/5
Воспользуемся формулой и найдем тангенс этого угла
Так как угол острый, то тангенс положителен.
Рассмотрим ΔKNF - прямоугольный
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
FN= HN- HF= 25-20 = 5 ед .
В ΔKNF- прямоугольном найдем гипотенузу по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов .
Рассмотрим хорды MN и KE . Произведение отрезков одной хорды равно произведению отрезков другой хорды .
Найдем отношение
Что и требовалось доказать.
б) Найдем площадь треугольника Δ KEN по формуле
где a и b - стороны треугольника, α - угол между ними.
∠FNE = ∠ KFM = α ( равны как вертикальные )
Найдем синус угла. Так как
Тогда площадь треугольника
Площадь треугольника Δ KEN равна 8,7 кв. ед.