Предмет: Алгебра,
автор: ramirr2006
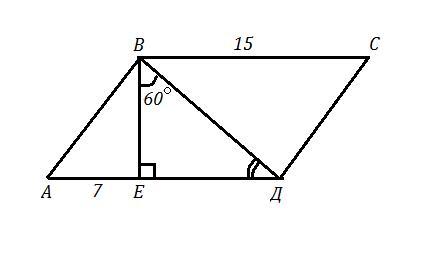
В параллелограмме ABCD на стороне AD отмечена точка E, AEB900,
EBD600, AЕ = 7 см, BC = 15 см. Найдите площадь параллелограмма.
Ответы
Автор ответа:
2
Ответ: S=40√3 см² .
АВСД - параллелограмм , ∠АЕВ=90° ⇒ ВЕ⊥АД , ВЕ - высота ,
ВС=АД=15 см , так как это противоположные стороны параллелограмма
ЕД=АД-АЕ=15-7=8 см
∠ЕВД=60° ⇒ в ΔВЕД угол ∠ВДЕ=90°-∠ЕВД=90°-60°=30° ⇒
В ΔВЕД : ВЕ=ЕД:tg60°=8:√3=8√3/3 cм .
S(АВСД)=АД*ВЕ=15*(8√3/3)=5*8√3=40√3 (см²)
Приложения:
101077:
NNNLLL54 можешь зайти на мой вопрос алгебра
во втором заданий найти остаток от деления многочлена х4-2х3+4х2-6х+8 на х-1
Похожие вопросы
Предмет: Технология,
автор: Zliliyaf7
Предмет: Русский язык,
автор: машенька1508
Предмет: Русский язык,
автор: Наташа252
Предмет: Алгебра,
автор: VeronikaShulga2000
Предмет: Французский язык,
автор: Люблюпоспать