Предмет: Геометрия,
автор: Аноним
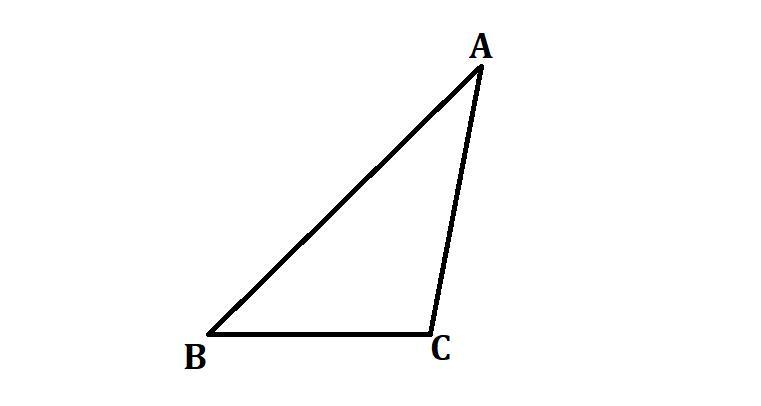
В треугольнике ABC угол А равен 45°, угол В равен 60°, ВС = 12√6. Найдите АС.
Ответы
Автор ответа:
7
Ответ:
36
Объяснение:
- Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Temnaaya
Предмет: Українська мова,
автор: 2007Никита
Предмет: Английский язык,
автор: Спитмаша
Предмет: Математика,
автор: Polinakorhagina
Предмет: Математика,
автор: denposkrebalov