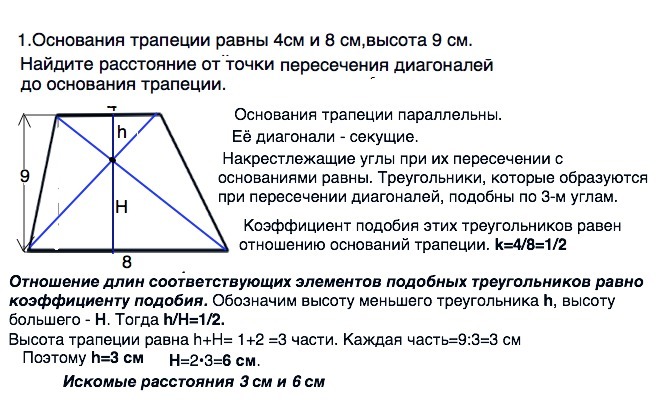
1.Основания трапеции равны 4см и 8 см,высота 9 см.Найдите расстояние от точки пересечения диагоналей до основания трапеции. 2.Два равнобедренных треугольника имеют равные углы,противолежащие основанию.В одном из треугольников боковая сторона и высота проведенная к основанию равны 5 см и 4 см.Найдите периметр второго треугольника,если боковая сторона равна 15 см.
Ответы
Основания трапеции параллельны.
Её диагонали - секущие.
Накрестлежащие углы при их пересечении с основаниями равны. Треугольники, которые образуются при пересечении диагоналей, подобны по 3-м углам.
Коэффициент подобия этих треугольников равен отношению оснований трапеции.
k=4/8=1/2
Отношение длин соответствующих элементов подобных треугольников равно коэффициенту подобия.
Точка пересечения диагоналей делит высоту трапеции на части, являющиеся высотами треугольников.
Обозначим высоту меньшего треугольника h, высоту большего - Н.
Тогда h/H=1/2.
Высота трапеции содержит 1+2 =3 части.
Каждая часть=9:3=3 см
Поэтому h=3 см
Н=2•3=6 см.
Расстояния от точки пересечения диагоналей до оснований трапеции равны 3 см и 6 см.
*****************
Задача 2.
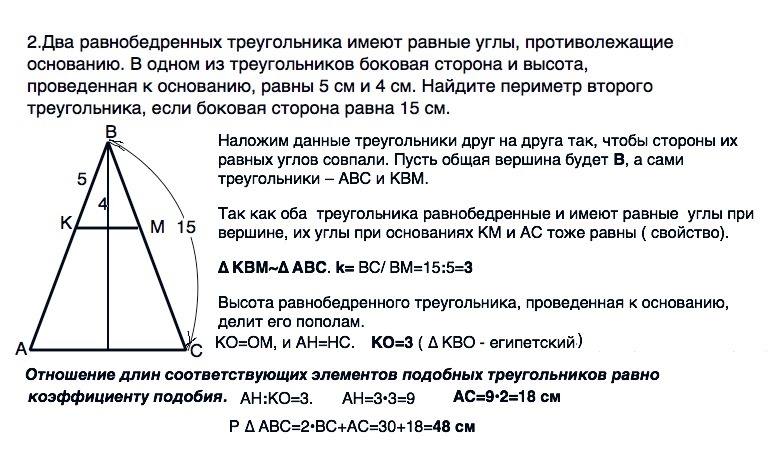
Наложим данные треугольники друг на друга так, чтобы стороны их равных углов совпали. Пусть общая вершина будет В, а сами треугольники – АВС и КВМ.
Так как оба треугольника равнобедренные и имеют равные углы при вершине, их углы при основаниях КМ и АС тоже равны ( свойство).
∆ КВМ~∆ АВС. k= ВС/ ВМ=15:5=3
Высота равнобедренного треугольника, проведенная к основанию, делит его пополам.
КО=ОМ, и АН=НС.
КО=3 ( ∆ КВО - египетский, проверьте по т.Пифагора.)
Отношение длин соответствующих элементов подобных треугольников равно коэффициенту подобия.
АН:КО=3.
АН=3•3=9
АС=9•2=18 см
Р ∆ АВС=2•ВС+АС=30+18=48 см