Найти производную срочноо
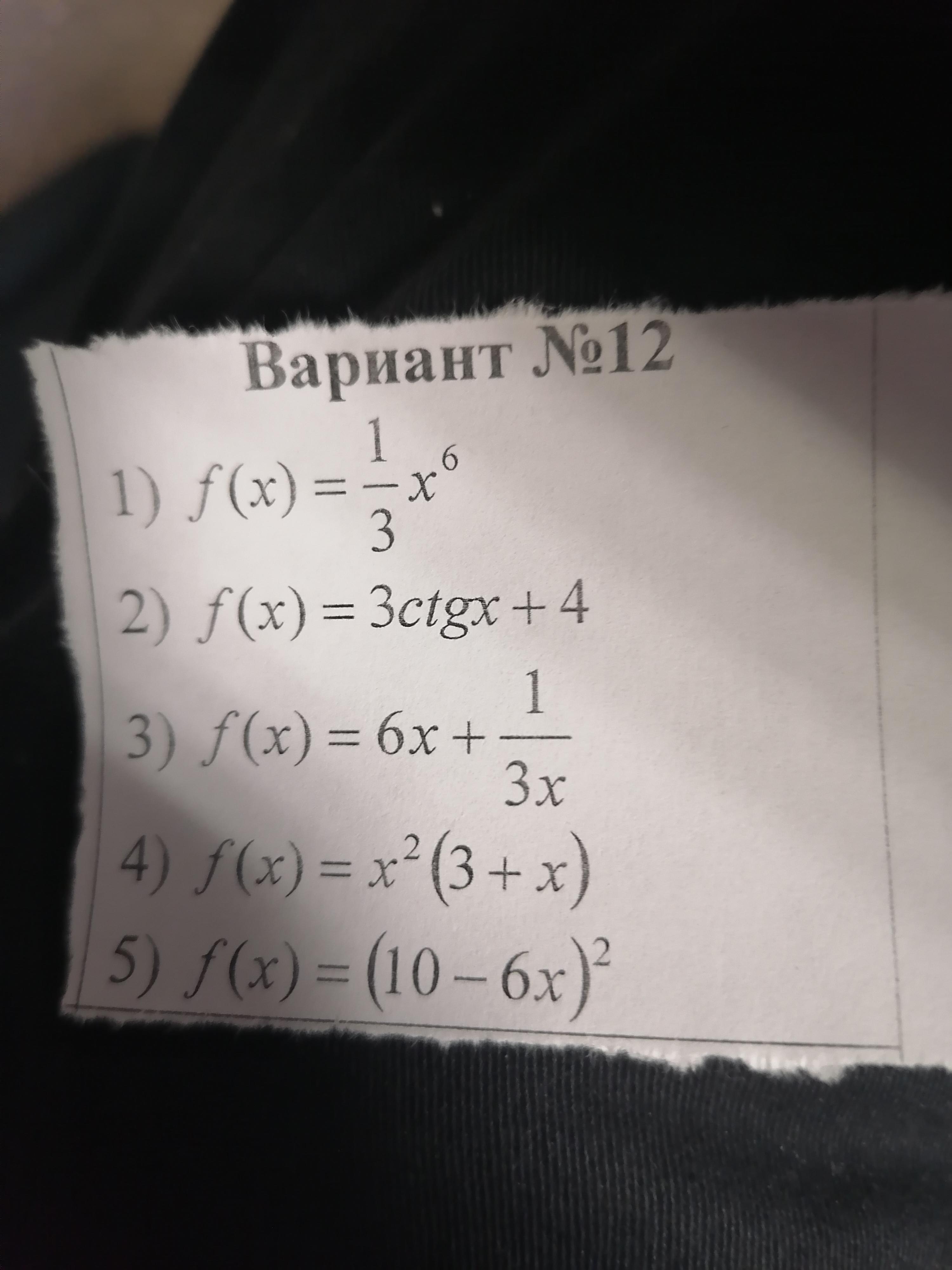
Ответы
Ответ:
)f
′
(x)=
3
1
×6x
5
=2x
5
\begin{gathered}2)f'(x) = - \frac{3}{ \sin {}^{2} (x) } \\ \end{gathered}
2)f
′
(x)=−
sin
2
(x)
3
\begin{gathered}3)f'(x) = (6x + \frac{1}{3} {x}^{ - 1} ) '= 6 + \frac{1}{3} \times ( - {x}^{ - 2} ) = \\ = 6 - \frac{1}{3 {x}^{2} } \end{gathered}
3)f
′
(x)=(6x+
3
1
x
−1
)
′
=6+
3
1
×(−x
−2
)=
=6−
3x
2
1
\begin{gathered}4)f'(x) = ( {x}^{2} (3 + x))' = (3 {x}^{2} + {x}^{3} )' = \\ = 6x + 3 {x}^{2} \end{gathered}
4)f
′
(x)=(x
2
(3+x))
′
=(3x
2
+x
3
)
′
=
=6x+3x
2
\begin{gathered}5)f'(x) = 2(10 - 6x) \times (10 - 6x)' = \\ = 2(10 - 6x) \times ( - 6) = \\ = - 12(10 - 6 x) = 72x - 120\end{gathered}
5)f
′
(x)=2(10−6x)×(10−6x)
′
=
=2(10−6x)×(−6)=
=−12(10−6x)=72x−120
Пошаговое объяснение:
Вот если не провильно то прости:(