Question

Дана функция f(x) = x² - 6x - 7
a) найдите вершину параболы;
b) постойте график функции;
c) определите область определения и множество значений функции;
d) определите ось симметрии;
e) определите промежутки монотонности (возрастания и убывания) функции.
Посогите срочно!!!!!!!!!!!!!!!! Пожалуйста​

Answer 1

Ответ:

Объяснение:

$f(x)=x^{2} -6x-7$

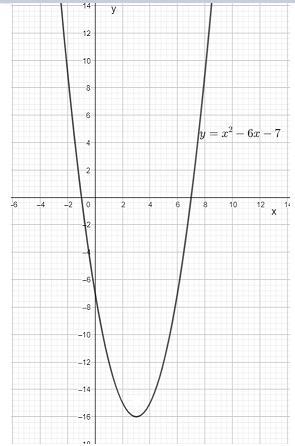
Графиком функции является парабола, ветви которой направлены вверх.

а)Найдем координаты вершины параболы.

$x{_0}=-\dfrac{b}{2a} ;\\\\x{_0}=-\dfrac{-6}{2\cdot1}=\dfrac{6}{2} =3;\\y{_0}= 3^{2} -6\cdot3-7=9-18-7=-16$

(3; -16) - вершина параболы .

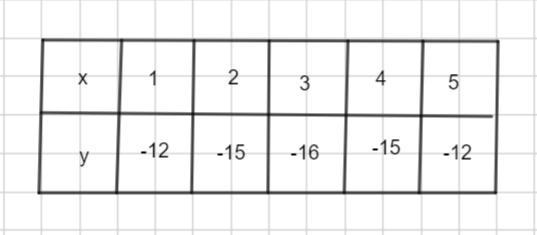
b) для построения графика составим таблицу значений.

Таблица значений и график функции во вложении.

c)

D(f)= (-∞; +∞) - область определения функции

E(f)= [-16; +∞) - множество значений функции.

d) x= 3 - ось симметрии

e) функция взрастает на [3; +∞)

функция убывает на (-∞; 3]