Предмет: Геометрия,
автор: togaaf
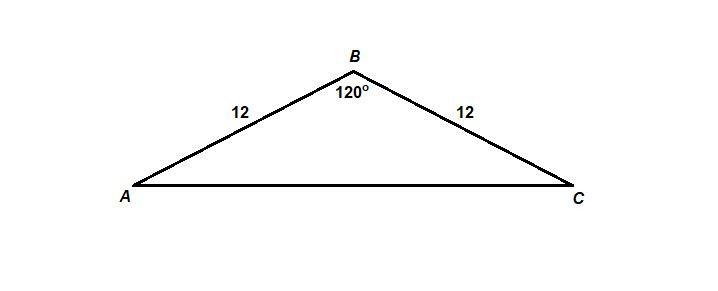
Боковая сторона АВ равнобедренного треугольника АВС равна 12 см,а угол противолежащей основанию АС,равен 120°.Найти радиус окружности,описанной около этого треугольника.
Ответы
Автор ответа:
14
Ответ:
12 см
Объяснение:
∠А = ∠С = (180° - ∠В) / 2 = (180° - 120°) / 2 = 60° / 2 = 30° как углы при основании равнобедренного треугольника.
По следствию из теоремы синусов:
где R - радиус описанной окружности.
см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: оскар4
Предмет: Русский язык,
автор: akrivopuskova
Предмет: Українська література,
автор: NIK1441
Предмет: Русский язык,
автор: 1234563434343
Предмет: История,
автор: valeriaaisha