Задачи на фото. Даю 25 баллов

Ответы
Ответ:
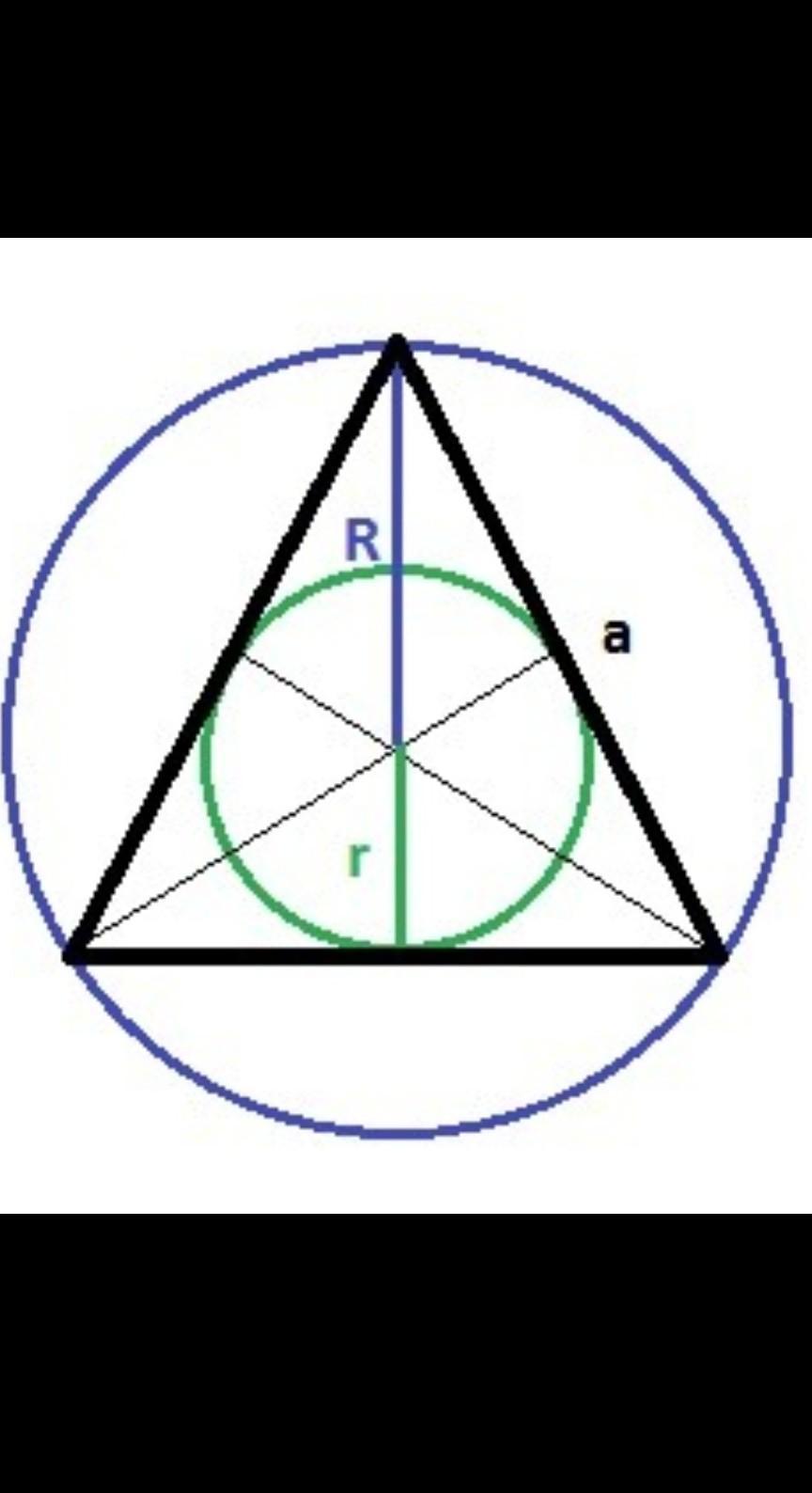
Центры описанной около равностороннего треугольника окружности и вписанной в равносторонний треугольник окружности совпадают с точкой пересечения медиан, высот, биссектрис. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. Поэтому радиусы так и будут относиться 2:1.
======================================
Можно найти отношение через формулы. Пусть сторона треугольника равна а. Тогда
R = \dfrac a{\sqrt3}R=
3
a
- радиус описанной окружности
r = \dfrac a{2\sqrt3}r=
2
3
a
- радиус вписанной окружности
\dfrac Rr=\dfrac a{\sqrt3}:\dfrac a{2\sqrt3}=\dfrac a{\sqrt3}\cdot \dfrac {2\sqrt3}a=2
r
R
=
3
a
:
2
3
a
=
3
a
⋅
a
2
3
=2
Радиус описанной окружности в 2 раза больше радиуса вписанной окружности.
Ответ: R : r = 2 : 1
Задача 2
2 и 3 картинки
Задача 3
4 картинка