Предмет: Алгебра,
автор: Nekiy04
Помогите решить пожалуйста, не понимаю
Приложения:
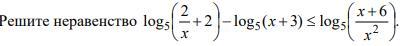
Ответы
Автор ответа:
1
Ответ:
ОДЗ:
С ОДЗ:
polinalyuft:
УМОЛЯЮ ТЕБЯ ПОМОГИ МНЕ ПОЖАЛУЙСТА
Похожие вопросы
Предмет: Английский язык,
автор: lalalap
Предмет: Окружающий мир,
автор: ceregakhramov
Предмет: Русский язык,
автор: бабушкаплатона
Предмет: Математика,
автор: Neymnica
Предмет: Математика,
автор: ChessMargarita