Question

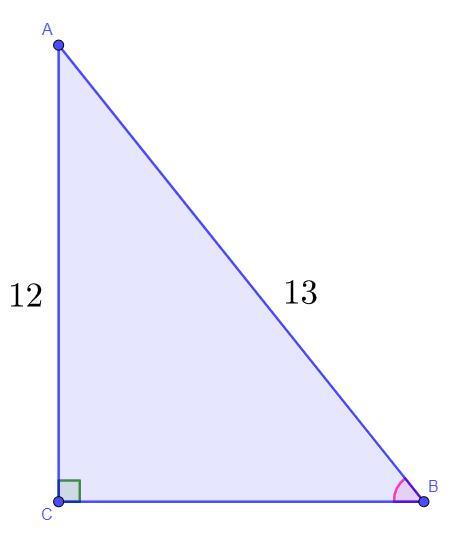
Дан треугольник ABC, у которого ∠C=90°.

vpr_m_8_130.svg

Найди третью сторону треугольника и ctg∠B, если известно, что AB=13, AC=12 см.

Ответ: третья сторона
см, ctg∠B =

Answer 1

Ответ:

$\boxed{BC = 5}$ см

$\boxed{\rm ctg \ \angle B = \dfrac{5}{12}}$

Объяснение:

Дано: ∠C = 90°, AB = 13 см, AC = 12 см

Найти: BC, ctg ∠B - ?

Решение:

Так как по условию угол ∠C = 90°, то треугольник ΔABC - прямоугольный, тогда по теореме Пифагора: $BC = \sqrt{AB^{2} - AC^{2}} = \sqrt{13^{2} - 12^{2}} = \sqrt{169 - 144} = \sqrt{25} = 5$ см.

По определению котангенса в прямоугольном треугольнике (ΔABC):

$\rm ctg \ \angle B = \dfrac{BC}{AC} = \dfrac{5}{12}$.