Question

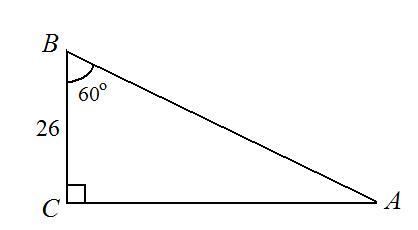
Помогите решить, пожалуйста. В треугольнике АВС, где ∠С=90°, ∠В=60°, СВ=26 см. Чему равна длина гипотенузы АВ?

Answer 1

Надо знать:

1) сумма острых углов прямоугольниого треугольника равна 90°;

2) в прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.

Поэтому:

пусть дан ΔАВС - прямоугольный, ∠В = 60°, СВ = 26 см. Найдем АВ.

∠А + ∠В = 90°, ∠В = 60°, значит, ∠А = 90° - 60° = 30°.

Тогда катет СВ лежит против угла в 30° и, следовательно, равен половине гипотенузы АВ, т.е. АВ = 2СВ = 2 · 26 = 52 (см).

Ответ: 52 см.