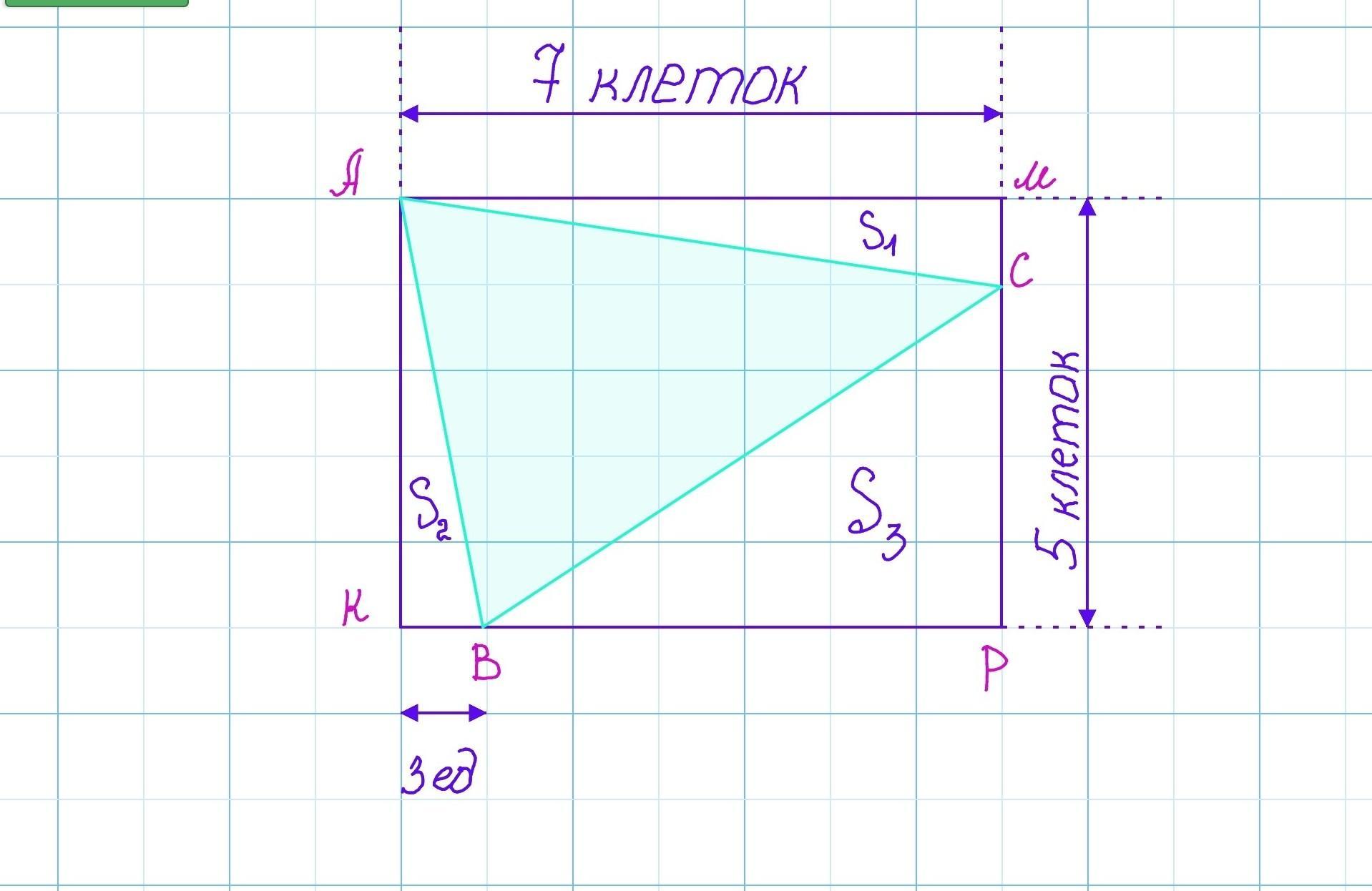
На бумаге в клетку нарисовали треугольник. Длина стороны клетки — 3 условных единиц. Найди площадь треугольника.
Очень срочно, пожалуйста!! 30 баллов!

Ответы
На бумаге в клетку нарисовали треугольник. Длина стороны клетки — 3 условных единиц. Найди площадь треугольника.
Ответ:
153 ед²
Объяснение:
Опишем вокруг ΔАВС прямоугольник АМРK.
Площадь ΔАВС будет равна: S(ΔАВС) = S(АМРK)-S₁-S₂-S₃.
Учтём, что длина стороны клетки 3 условные единицы.
1) Для вычисления площади прямоугольника нужно умножить его длину на ширину.
AМ = 7 клеток = 7•3 =21 ед
AК = 5 клетoк = 5•3 =15 ед
S(АМРK) = АМ·АК = 21•15 = 315 ед²
2) Площадь прямоугольного треугольника равна половине произведения его катетов.
S₁ = ½ *АМ*МС
АМ = 7 клетoк = 7•3 = 21 ед
МС = 1 клетка = 1•3 =3 ед
S₁= ½ *21*3 = 31,5 ед²
S₂ = ½ *АК*КВ
АК = 5 клетoк = 5•3 = 15 ед
KВ = 1 клеткa = 1•3 = 3 ед
S₂ = ½ *15*3 = 22,5 ед²
S₃ = ½ *ВР*СР
ВР = 6 клеток = 6•3 = 18 ед
СР = 4 клетки = 4•3 = 12 ед
S₃ = ½ *18*12 = 108 ед²
Итак, S(ΔАВС) = S(АМРK)-S₁-S₂-S₃= 315-31,5-22,5-108 = 153 ед²