Question

Две хорды окружности взаимно перпендикулярны. Докажите,
что расстояние от центра окружности до точки их пересечения равно
расстоянию между серединами этих хорд, даю 25 баллов

Answer 1

Ответ:

Объяснение:

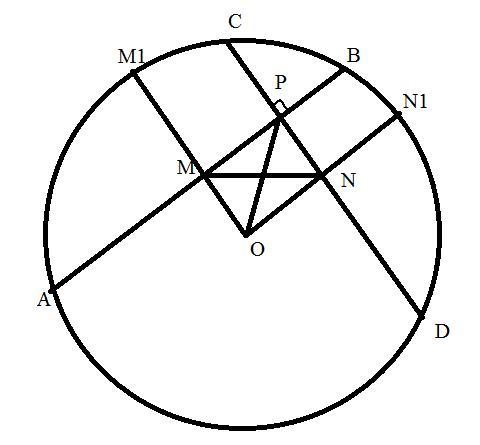
Пусть АВ и CD - хорды, перпендикулярные друг к другу, пересекающиеся в точке Р. Точки M и N - середины хорд АВ и CD.

Проведём радиусы ОМ1 и ОN1 через эти точки M и N. Эти радиусы будут перпендикулярны хордам АВ и CD соответственно по свойству хорды и радиуса (ну или доказывается через равнобедренный треугольник с боковыми сторонами, равными радиусу и медианой, проведённой к основанию - она же будет высотой).

Значит <OMP=<ONP=90°, при этом <MPN=90° по условию. Значит в четырёхугольнике OMPN оставшийся 4й угол <MON также равен 90° => OMPN - прямоугольник. В прямоугольнике диагонали равны, значит OP=MN, чтд.