Question

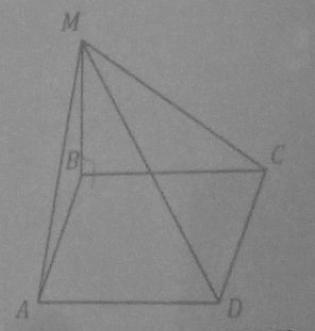
Задача из вершины B прямоугольника ABCD восстановлен перпендикуляр MB к плоскости прямоугольника Расстояние от точки M до остальных вершин прямоугольника равны 6см, 7см и 9см надите длину перпиндикуляр MB
Решение:
Пусть AB

Answer 1

Ответ: МВ=2 см

Объяснение:

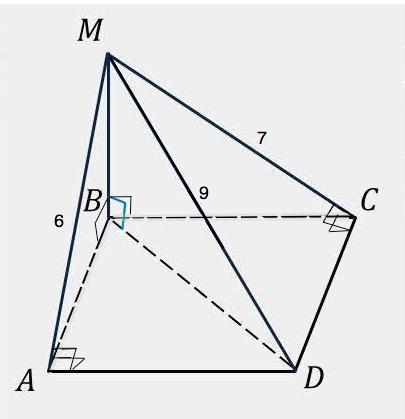
      АВСD– прямоугольник. Проекции наклонных МА и МС перпендикулярны АD и СD. По т. о 3-х перпендикулярах наклонные МА и МС перпендикулярны АD и СD соответственно =>

∆ МАD – прямоугольный. По т.Пифагора AD²=MD²-MA²=81-36=45

∆ MCD – прямоугольный. По т.Пифагора DС²=MD²-MC²=81-49=32

Диагональ прямоугольника делит его на равные прямоугольные треугольники. => АВ=CD.

По т.Пифагора BD²=DC²+AD²=32+45=77

MB⊥BD => ∆ MBD – прямоугольный.

По т.Пифагора MB²=MD²-BD²=81-77=4=>

MВ=√4=2 см.