Question

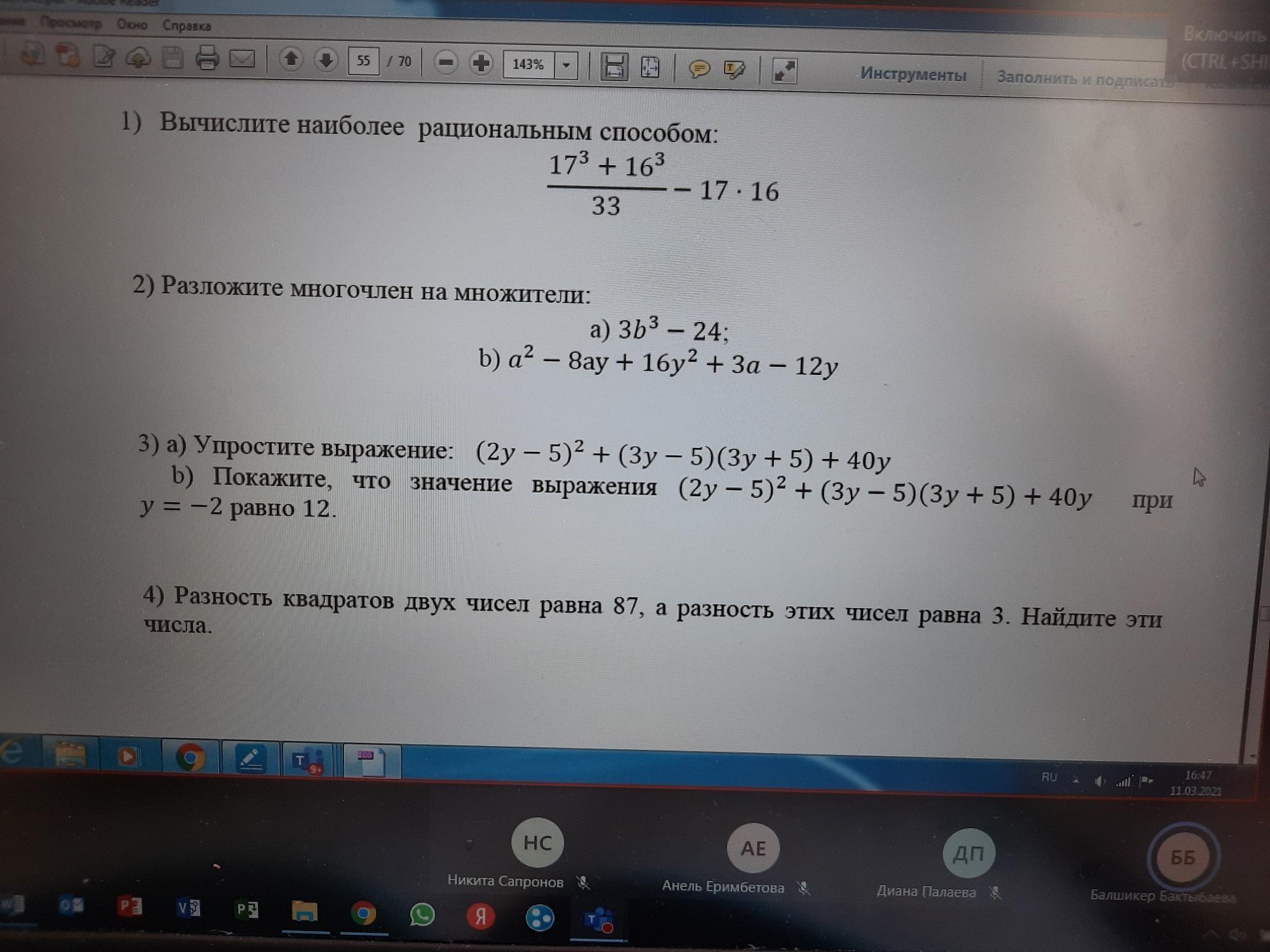
1.вычислите наиболее рациональным способом
2.Разложите многочлен на множители
3.(а)Упростите выражение(b)Покажите, что значение выражения при y=-2 равно 12
4.Разность квадратов двух чисел равна 87, а разность этих чисел равна 3.Найдите эти числа

Answer 1

Ответ и объяснение:

Нужно знать формулы сокращённого умножения

1a) x³ + y³ = (x + y)·(x² - x·y + y²);

1b) (x - y)² = x² - 2·x·y + y²;

2a) x³ - y³ = (x - y)·(x² + x·y + y²);

3a) x² - y² = (x - y)·(x + y);

1) Вычислите наиболее рациональным способом

$\dfrac{17^3+16^3}{33}-17 \cdot 16.$

Применим формулы 1a) и 1b):

$\dfrac{17^3+16^3}{33}-17 \cdot 16 = \dfrac{(17+16) \cdot (17^2-17 \cdot 16+16^2)}{33}-17 \cdot 16 =\\\\= \dfrac{33 \cdot (17^2-17 \cdot 16+16^2)}{33}-17 \cdot 16 = 17^2-17 \cdot 16+16^2-17 \cdot 16=\\\\= 17^2-2 \cdot 17 \cdot 16+16^2 =(17-16)^2=1^2=1.$

2) Разложите многочлен на множители

a) 3·b³ - 24;

b) a² - 8·a·y + 16·y² + 3·a - 12·y.

Применим формулу 2a):

a) 3·b³ - 24 = 3·(b³ - 8) = 3·(b³ - 2³) = 3·(b - 2)(b² + 2·b + 4);

Применим формулу 1b):

b) a² - 8·a·y + 16·y² + 3·a - 12·y = a² - 2·a·4·y + (4·y)² + 3·(a - 4·y) =

= (a - 4·y)² + 3·(a - 4·y) = (a - 4·y)·(a - 4·y + 3).

3) a) Упростите выражение

(2·y - 5)² + (3·y - 5)·(3·y + 5) + 40·y;

b) Покажите, что значение выражения (2·y - 5)² + (3·y - 5)·(3·y + 5) + 40·y при y = -2 равно 12.

Применим формулы 1b) и 3a):

(2·y - 5)² + (3·y - 5)·(3·y + 5) + 40·y = 4·y² - 20·y + 25 + 9·y² - 25 + 40·y =

= 13·y² + 20·y;

Подставим в последнее выражение значение y = -2 и получим:

b) 13·(-2)² + 20·(-2) = 13·4 - 20·2 = 52 - 40 = 12.

4) Разность квадратов двух чисел равна 87, а разность этих чисел равна 3. Найдите эти числа.

Решение. Пусть x первое число, а y второе число. По условию

x² - y² = 87 и x - y = 3.

Применим формулу 3a) для квадратов чисел и учитывая второе равенство получим:

x² - y² = 87 ⇔ (x - y)·(x + y) = 87 ⇔ 3·(x + y) = 87 ⇔ x + y = 29.

Решим систему уравнений:

$\displaystyle \tt \left \{ {{x+y=29} \atop {x-y=3}} \right. \Leftrightarrow \left \{ {{y=29-x} \atop {x-(29-x)=3}} \right. \Leftrightarrow \left \{ {{y=29-x} \atop {x-29+x=3}} \right. \Leftrightarrow \\\\\Leftrightarrow \left \{ {{y=29-x} \atop {2 \cdot x=3+29}} \right. \Leftrightarrow \left \{ {{y=29-x} \atop {2 \cdot x=32}} \right. \Leftrightarrow \left \{ {{y=29-16=13} \atop {x=16}} \right. .$

Искомые числа 16 и 13.