Предмет: Алгебра,
автор: artyrchik228
Найдите:
tga, если sin a = 12/13, п/2 < а < п
Приложения:
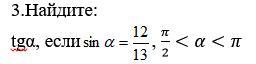
Ответы
Автор ответа:
2
Ответ: -2,4.
Объяснение:
Найти
tga, если sin a = 12/13, п/2 < а < п
--------------
cosa=√1-sin²a = √1-(12/13)² = √1-144/169=√25/169 =5/13;
tga = sina/cosa = 12/13 : 5/13 = 12/13 * 13/5 = 2,4.
---------------
п/2 < а < п - II четверть. Тангенс во 2 четверти отрицательный:
Ответ: tga = -2,4.
Автор ответа:
5
Объяснение:
Ответ: tgα=-2,4.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: lisenok80
Предмет: Русский язык,
автор: marimari991
Предмет: Русский язык,
автор: GlebRald
Предмет: Алгебра,
автор: Donaticher