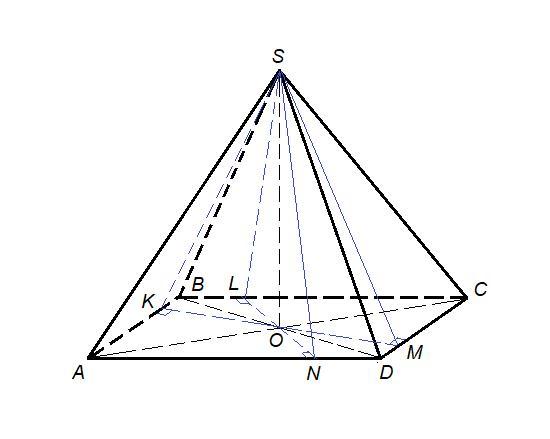
Дана пирамида, у которой все боковые грани с плоскостью основания образуют равные углы.
КакиИЕ из утвержденИЙ верны?
вершина пирамиды проецируется в точку пересечения биссектрис основания
основанием пирамиды может быть ромб
все высоты боковых граней равны
данная пирамида — правильная
Ответы
Ответ:
Верные утверждения:
Вершина пирамиды проецируется в точку пересечения биссектрис основания.
Основанием пирамиды может быть ромб.
Все высоты боковых граней равны.
Объяснение:
- Если боковые грани пирамиды образуют с плоскостью основания равные углы, то высота проецируется в центр окружности, вписанной в основание.
Докажем это утверждение.
SO - высота пирамиды. Проведем перпендикуляры из точки О к ребрам основания - OK, OL, OM и ON.
Эти отрезки - проекции наклонных SK, SL, SM и SN, значит и наклонные перпендикулярны ребрам основания по теореме о трех перпендикулярах.
Тогда ∠SOK = ∠SOL = ∠SOM = ∠SON - линейные углы двугранных углов при ребрах основания.
ΔSOK = ΔSOL = ΔSOM = ΔSON по катету и противолежащему острому углу:
- эти треугольники прямоугольные, так как SO высота;
- SO - общий катет;
равные углы указаны выше.
Значит, OK = OL = OM = ON, то есть точка О равноудалена от сторон основания, значит это центр окружности, вписанной в основание.
Из равенства треугольников следует так же равенство высот боковых граней: SK = SL = SM = SN.
______________________________________________
Итак, рассмотрим данные утверждения:
Вершина пирамиды проецируется в точку пересечения биссектрис основания.
Верно. Так как центр вписанной в основание окружности - точка пересечения биссектрис.
Основанием пирамиды может быть ромб.
Верно, так как в ромб можно вписать окружность.
Все высоты боковых граней равны.
Верно. Доказано выше.
Данная пирамида — правильная.
Неверно. В основании может быть любой многоугольник, в который можно вписать окружность.