Предмет: Алгебра,
автор: 23ukraina2003
Вычислить за формулой Муавра
Приложения:
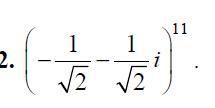
Ответы
Автор ответа:
0
Запишем число z в показательной форме:
Поскольку число z находится в III четверти, то
тогда
теперь возведем в степень
Похожие вопросы
Предмет: Русский язык,
автор: po4ik
Предмет: Русский язык,
автор: Бэт12345
Предмет: Другие предметы,
автор: ltkvf1981
Предмет: Физика,
автор: Lizagaga