Предмет: Алгебра,
автор: dizzysun
записать уравнение касательной, проведенной к графику функции:
f(x) = x^2-2x+3
x0 = 3
пожалуйста, через фотомач не добавляйте или же другие задания!! у меня контрольная работа.
Приложения:
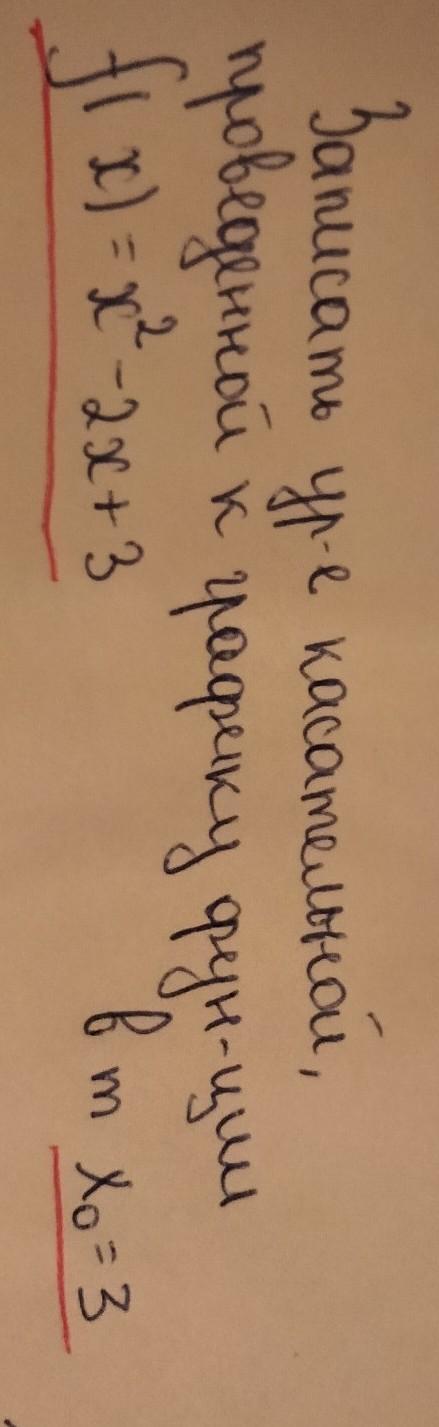
Ответы
Автор ответа:
2
Уравнение касательной к графику функции в точке имеет вид:
.
Итак, для начала высчитаем . Чтобы сделать это, просто подставим в нашу функцию вместо
значение
.
.
Теперь найдём производную этой функции.
Теперь вычислим . То же самое - подставляем в производную вместо
значение
.
.
Теперь вернёмся к уравнению касательной, написанному выше, и подставим туда вычисленные величины.
Похожие вопросы
Предмет: Русский язык,
автор: таня8922852
Предмет: Русский язык,
автор: gkirdplay
Предмет: Английский язык,
автор: desert3
Предмет: Биология,
автор: АнджелинаLove