Предмет: Геометрия,
автор: Аноним
ПРОШУ ПОМОГИТЕ!!..
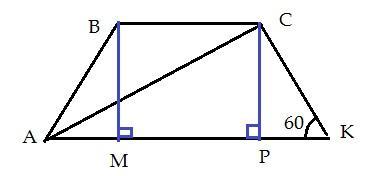
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь трапеции, если большее основание равно 8v3, а один из углов трапеции равен 60 градусов.
Ответы
Автор ответа:
1
Ответ:
72 см²
Объяснение:
1. Прямоугольный Δ АСК. ∠ К = 60° ⇒ ∠А = 180 - 90 - 60 = 30° ⇒ СК = 1/2АК = 4√3, как катет, лежащий напротив угла в 30°.
2. Прямоугольный Δ СРК. ∠К = 60° ⇒ ∠ С = 180 - 90 - 60 = 30°
⇒ РК = 1/2 СК = 2√3, как катет, лежащий напротив угла в 30°.
По теореме Пифагора СР = √(СК² - РК²) = √36 = 6
3. Δ АВМ = Δ СРК по гипотенузе и острому углу ⇒ АМ = РК = 2√3 ⇒ МЗ = 8√3 - 2√3 - 2√3 = 4√3.
4. В 4-х угольнике ВСРМ противоположные стороны попарно параллельны, углы = 90° ⇒ является прямоугольником. ⇒ ВС = МР = 4√3
5. S трапеции АВСК = СР * (ВС + АК)/2 = 6 * (4√3 + 8√3) = 72√3 см²
Приложения:
nike77514:
это правильно ?
Похожие вопросы
Предмет: Українська мова,
автор: marcurkan
Предмет: Английский язык,
автор: настя495
Предмет: Русский язык,
автор: viktor5sokol
Предмет: Другие предметы,
автор: tourss