Предмет: Математика,
автор: misham2904
Срочно! Тригонометрическое уравнение! 20 баллов!
Найди корни уравнения:

Где:

Приложения:
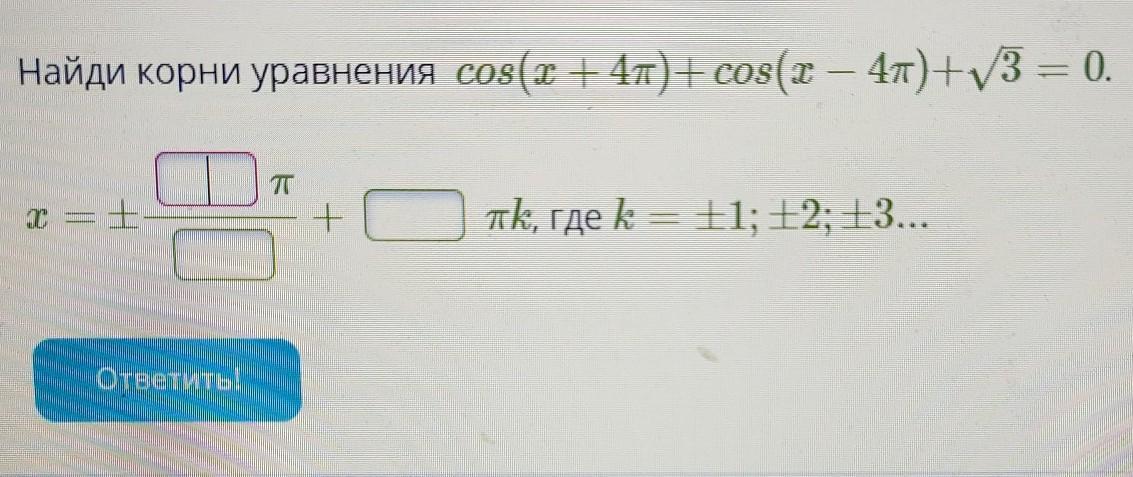
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
4П - период косинуса, поэтому он не влияет на аргумент, значит
cos(x+4П)+cox(x-4П)+√3=0 это то же самое, что
cosx+cosx+√3=0
2cosx=-√3
cosx=-√3/2,
х=±5π/6+2πk
misham2904:
НЕПРАВИЛЬНО! Ответ: x=±5π/6+2πk, где k...
Неясно, откуда взялось +-п, а так решение легче для восприятия, чем моё )
Автор ответа:
1
Ответ:
Я не понимаю, почему у вас там не включен ноль в решения, пробуйте забить так, хоть у вас и не Z...
Ответ верен
Пошаговое объяснение:
см. закреп
Приложения:
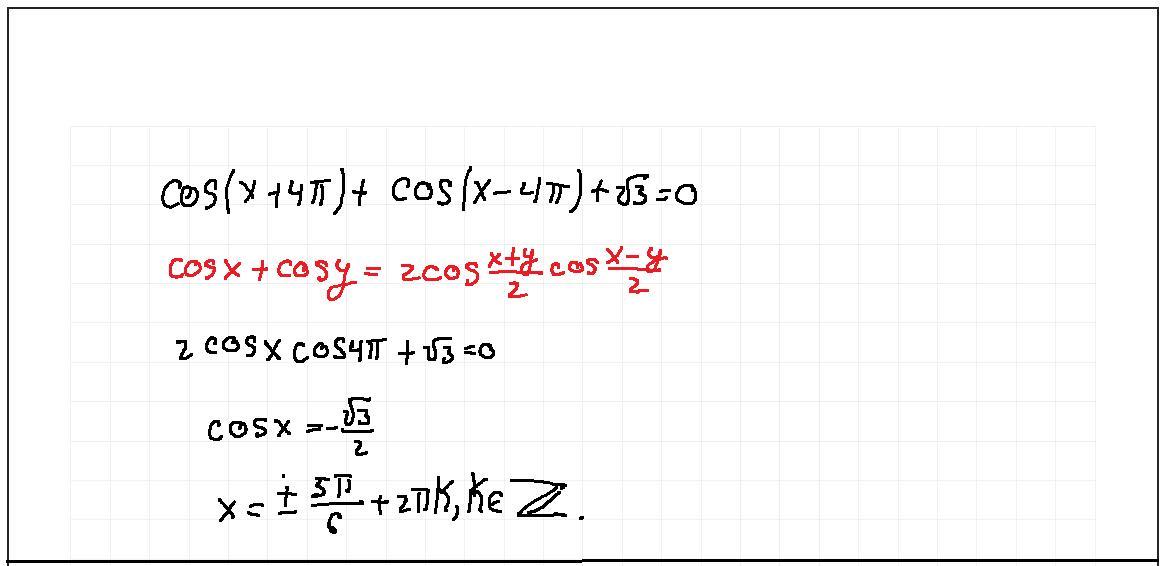
Похожие вопросы
Предмет: Русский язык,
автор: влвтлцлыстчттв
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: kotenokmur86
Предмет: Английский язык,
автор: austinova578
Предмет: Литература,
автор: NASTYA2648234