Предмет: Геометрия,
автор: bajkenovaaruzan
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь трапеции, если большее основание равно 8√3, а один из углов трапеции равен 600.
АД=8√3
LA=LД=60°
Приложения:
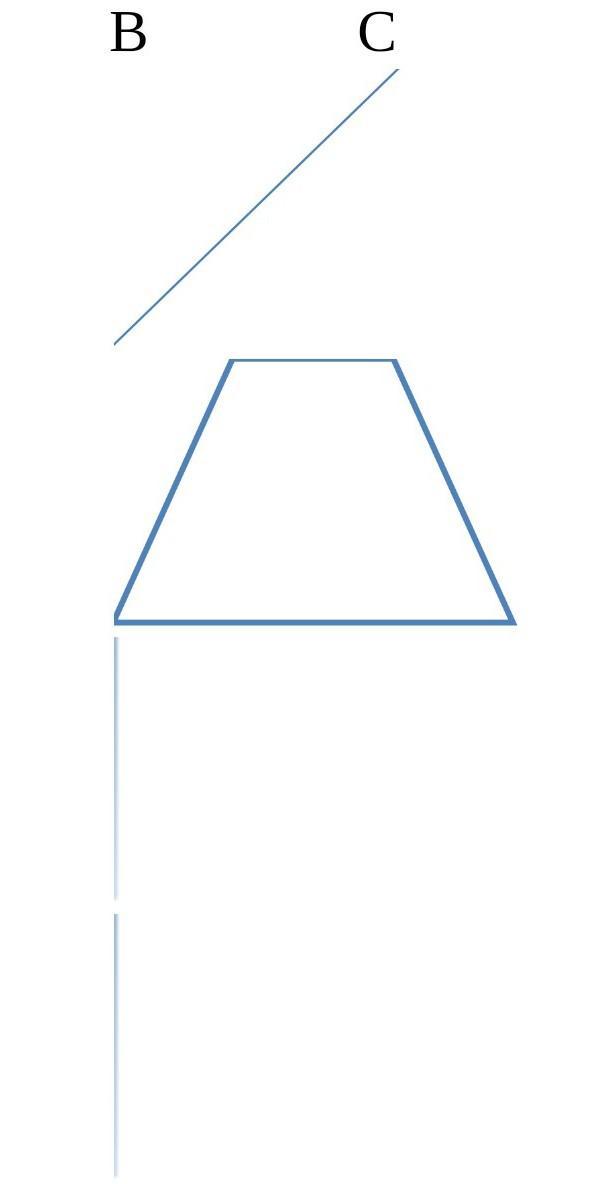
Ответы
Автор ответа:
0
Ответ: 36√3.
Объяснение:
Решение.
Диагональ в равнобедренной трапеции перпендикулярная боковой стороне отсекает равнобедренный треугольник АВС - АВ=ВС=CD.
Угол CAD = 30°.
Находим боковую сторону:
CD=AD*sin30°=8√3*1/2 = 4√3.
АВ=ВС=CD=4√3.
------------
Проведем высоту CE.
CE=h=CD*cos30°=4√3*√3/2 = 2*3=6.
--------------------
Площадь S =h(a+b)/2 = 6(4√3+8√3)/2 = 3*12√3 = 36√3.
Похожие вопросы
Предмет: Русский язык,
автор: Paulina11
Предмет: Окружающий мир,
автор: микс8
Предмет: Другие предметы,
автор: naymenko500
Предмет: История,
автор: VikaKalechits