Предмет: Алгебра,
автор: ssjjajsks
срочно!!! помогите пожалуйста сделать
Приложения:
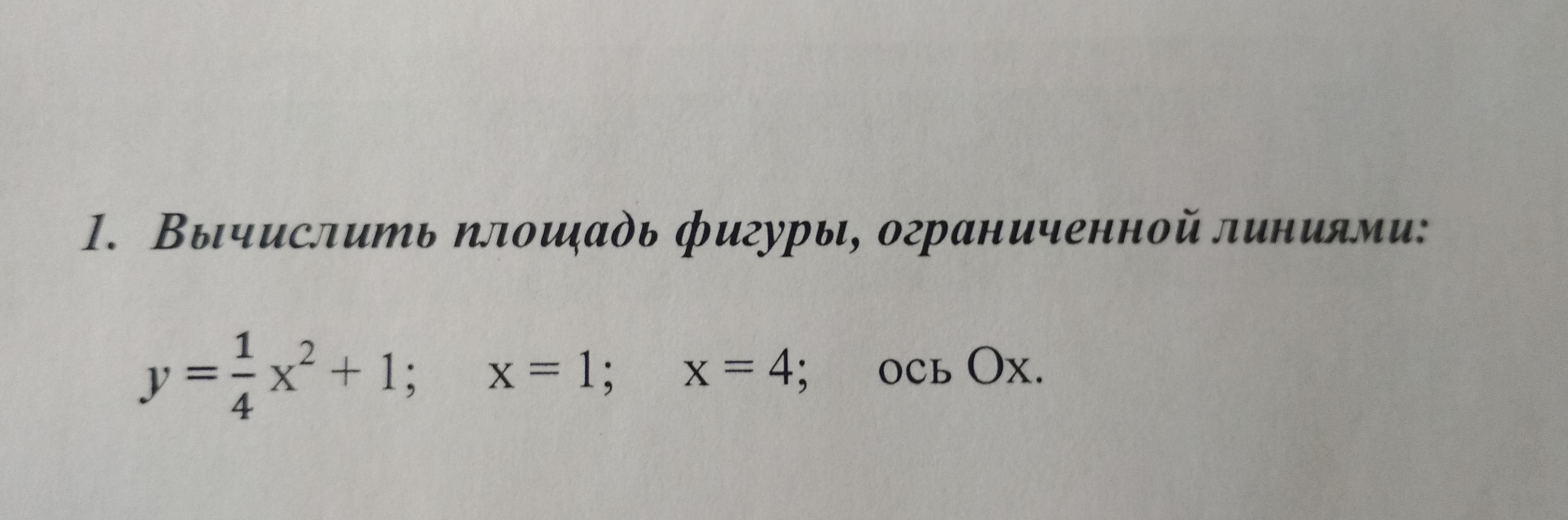
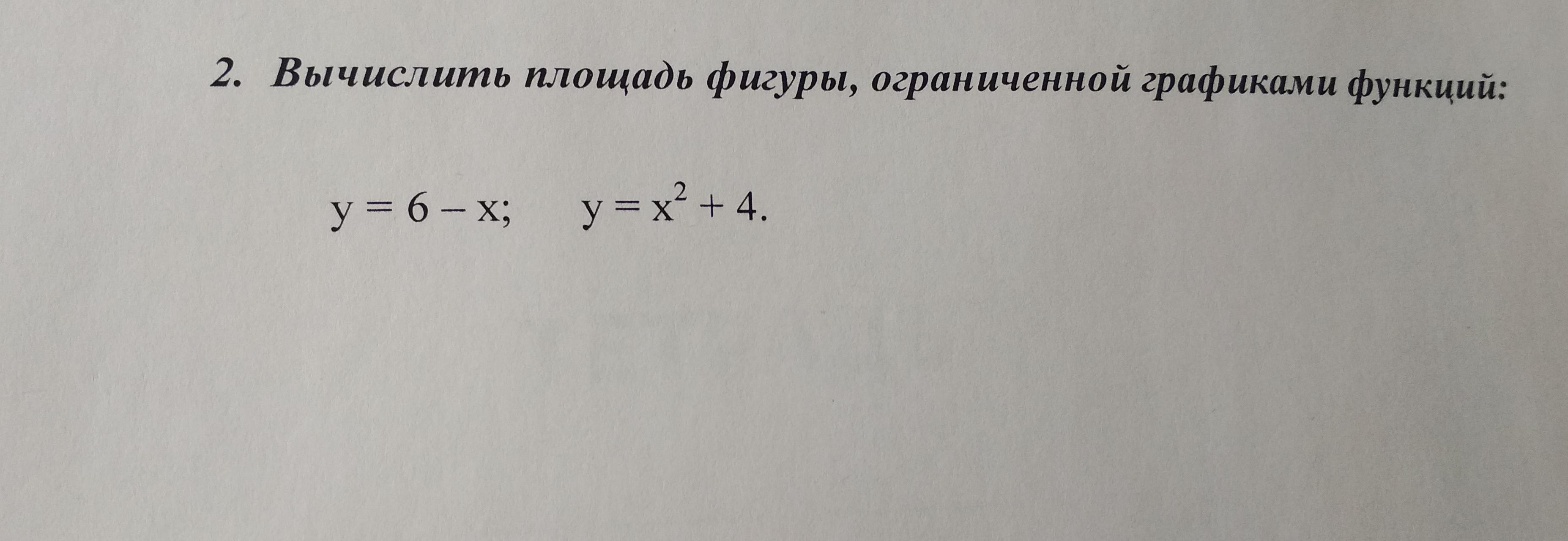
Ответы
Автор ответа:
1
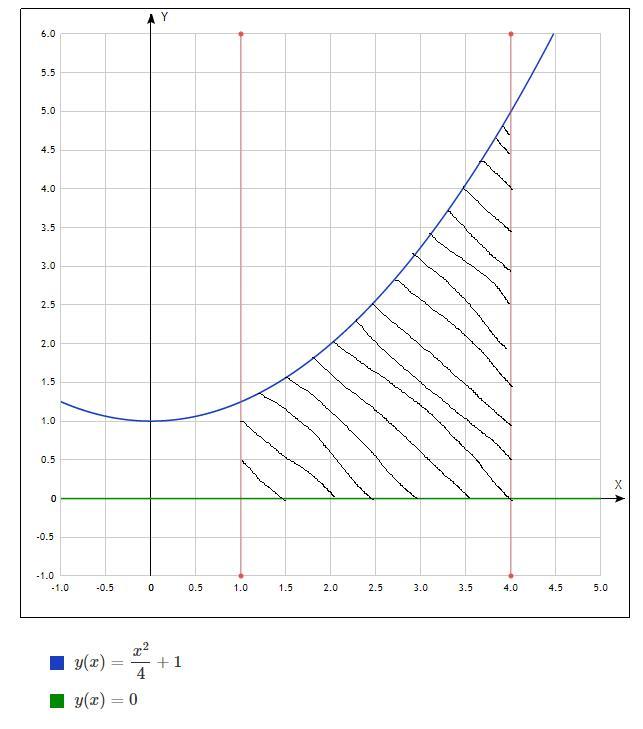
1.
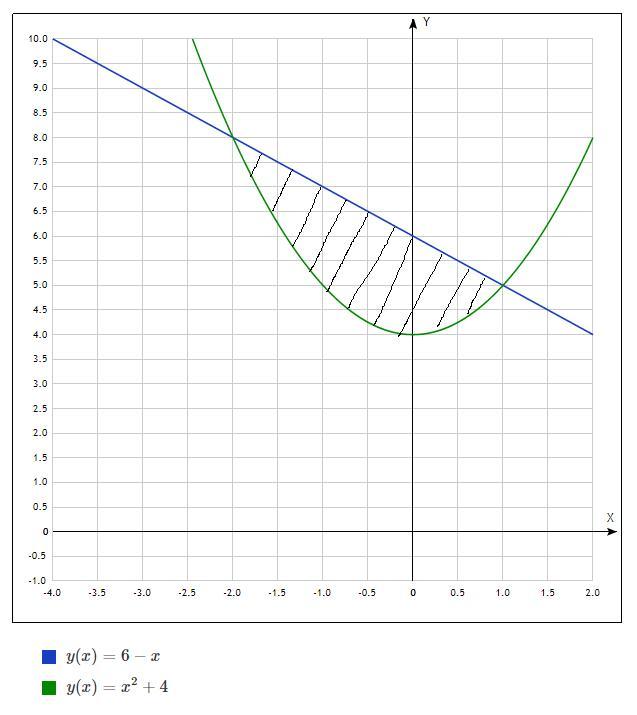
2.
Приложения:
ssjjajsks:
а можно график к первому?
Похожие вопросы
Предмет: Русский язык,
автор: kartmambetovar
Предмет: Технология,
автор: varvaraurina
Предмет: Қазақ тiлi,
автор: лиза139ен
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: vanykazakoff