Предмет: Алгебра,
автор: ytsergey65
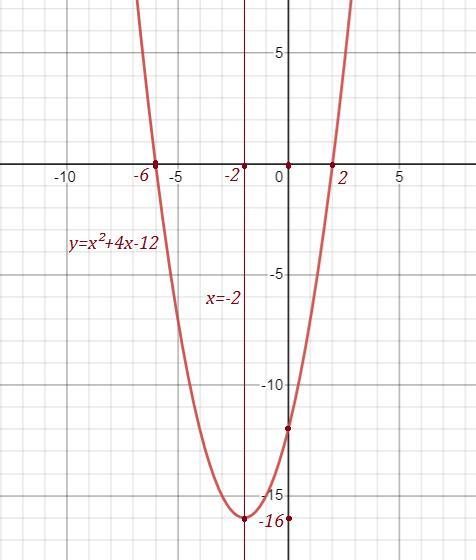
Функция задана уравнением у=х^2+4x-12
a) В какой точке график данной функции пересекает ось ОY?
[1]
b) Найдите точки пересечения графика функции с осью ОХ.
[2]
c) Запишите уравнение оси симметрии графика данной функции.
[1]
d) Найдите наибольшее или наименьшее значение функции.
СРОЧНО !!!!!!!
Ответы
Автор ответа:
2
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: dobryykirya
Предмет: Русский язык,
автор: malievaaliskaalisa
Предмет: Литература,
автор: kindar01
Предмет: Биология,
автор: Tomik1320