Предмет: Геометрия,
автор: dkarelov133
Помогите пожалуйста даю 100 баллов решить нужно срочно
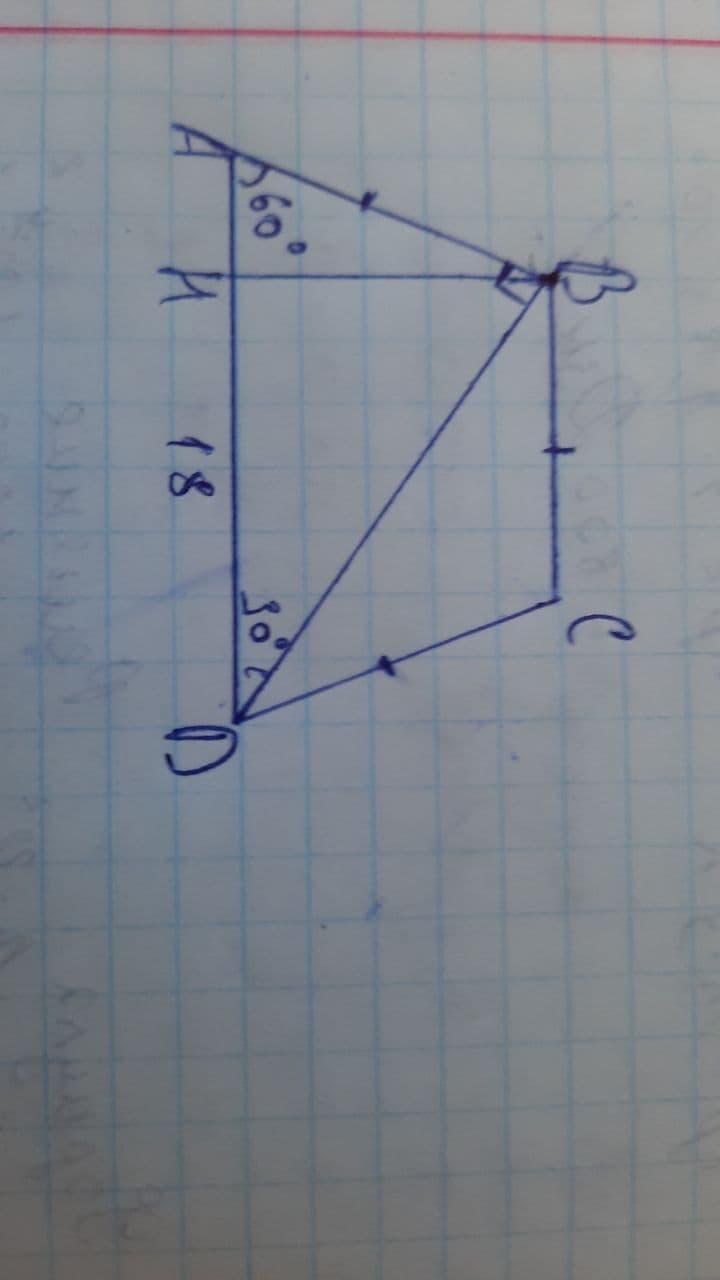
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь трапеции, если большее основание равно 18, а один из углов трапеции равен 60градусов
Ответы
Автор ответа:
2
Ответ:
105,222105cm^2
Объяснение:
Дано:
ABCD-равнобедренная трапеция
AB=CD
∠A=60
AD=18
Найти:
S
Решение:
т.к ABD прямоугольный
∠BDA=180-(60+90)=30
тогда BA равен половине гипотенузе т.к противолежит углу 30 градусов
BA=AD/2=18/2=9
т.к BD перпендикулярна боковой стороне и делит угол D пополам
AB=BC
Высота трапеции равна половине диагонали
т.к противолежит углу 30 градусов
BD^2=18^2-9^2=243
BD=√243=9√3
BH=
S=cm^2
Приложения:
lochgipon:
щас рисунок прикреплю
Спасибо большое
Похожие вопросы
Предмет: Українська мова,
автор: TaniaBobliah25
Предмет: Русский язык,
автор: Sofika20137
Предмет: Английский язык,
автор: Lena300804
Предмет: Алгебра,
автор: davidkhatkintop
Предмет: Алгебра,
автор: Gurskaya56