Предмет: Геометрия,
автор: 050307andry
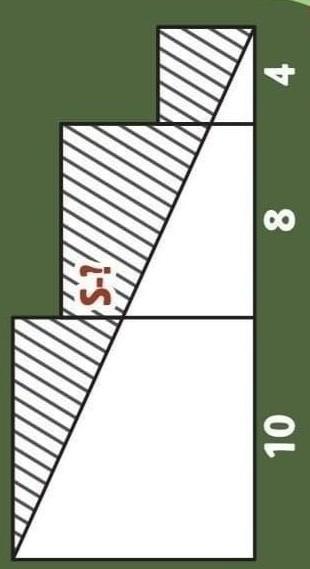
Перед вами фигура, состоящая из трех квадратов. Найдите площадь заштрихованной фигуры. С пошаговым объяснением.
Приложения:
Ответы
Автор ответа:
0
Ответ:
Площадь заштрихованной фигуры равна 70
Объяснение:
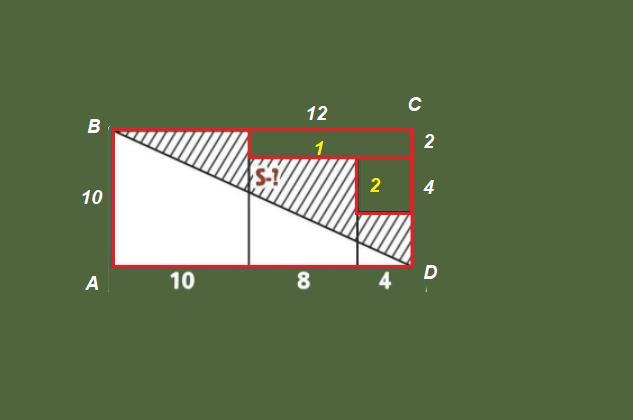
Достроим прямоугольник ABCD.
АВ = 10 - сторона большего квадрата.
ВС = 10 + 8 + 4 = 22 - сумма длин сторон всех трех квадратов.
Тогда его площадь:
- Диагональ делит прямоугольник на два равных прямоугольных треугольника.
Тогда площадь треугольника BCD:
Чтобы найти площадь заштрихованной фигуры, надо из площадь треугольника BCD вычесть площади прямоугольников 1 и 2.
Стороны прямоугольника 1:
10 - 8 = 2
8 + 4 = 12
Площадь прямоугольника 1:
Стороны прямоугольника 2:
8 - 4 = 4
вторая сторона равна стороне меньшего квадрата, 4.
То есть, это получился квадрат.
Его площадь:
Итак, площадь заштрихованной фигуры:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: джанико
Предмет: Другие предметы,
автор: ykov200403021
Предмет: Русский язык,
автор: помошник10
Предмет: Английский язык,
автор: mishina2007
Предмет: Химия,
автор: JuliaVang5