Question

....................... ​

Answer 1

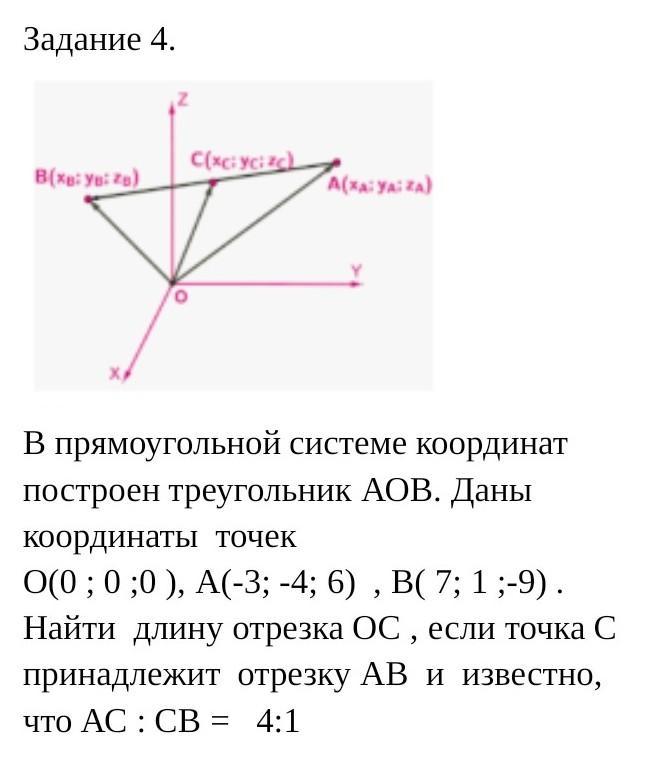
Даны координаты точек: O(0; 0; 0), A(-3; -4; 6), B(7; 1; -9).

Точка С делит отрезок АВ в отношении 4 : 1, то есть на 5 частей.

Отрезок АС составляет(4/5) длины АВ.

Находим разность координат АВ: (10; 5; -15).

Определяем приращение координат от точки А до точки С.

Δx = 10*(4/5) = 8,

Δy = 5*(4/5) = 4,

Δx = -15*(4/5) = -12.

Теперь находим координаты точки С.

xC = -3+8 = 5.

yC = -4+4 = 0,

zC = 6+(-12) = -6.

Так как точка О имеет нулевые координаты, то вектор ОС численно равен координатам точки С.

Ответ: ОС = √(5² + 0² + (-6)²) = √(25 + 0 + 36) = √61 ≈ 7,81025.

Есть формула для определения координат точки при деление отрезка

в данном отношении.

хС = (xA + λ*xB)/(1 + λ). где λ - отношение АС к СВ.