Предмет: Математика,
автор: Xterwel
Вычислить частную производную функции:
Приложения:
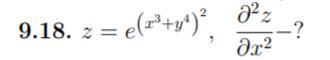
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: imavetkapm97
Предмет: Русский язык,
автор: мари44
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: shahriyorchikozb8ts
Предмет: Химия,
автор: ДобрыйДядяУсач