Предмет: Математика,
автор: Аноним
Помогите решить пожалуйста.Буду благодарен
Приложения:
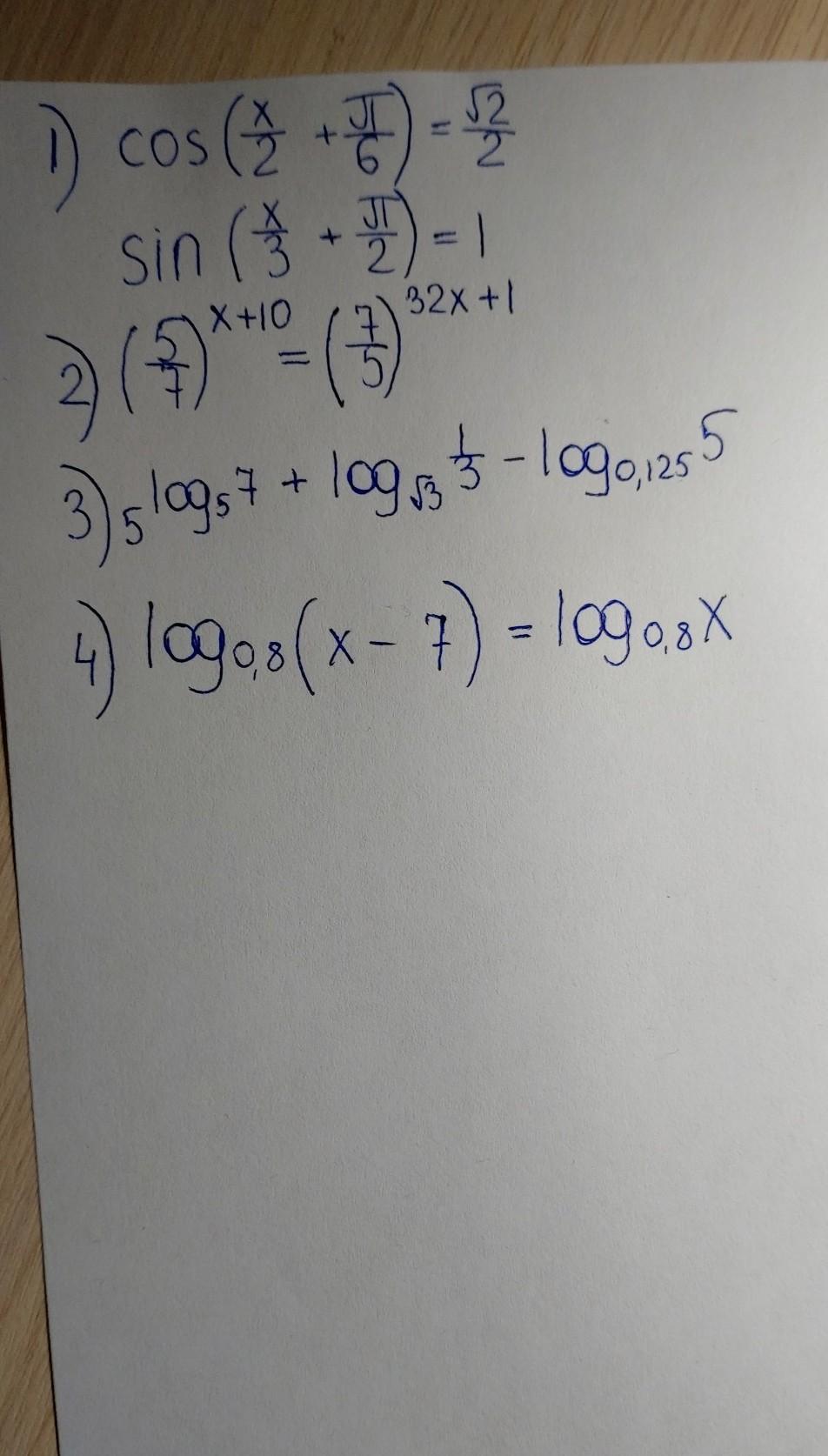
MatemaU9:
если не секрет,то какой это класс?
Ответы
Автор ответа:
2
Ответ:
1
n принадлежит Z
n принадлежит Z.
2.
3.
4.
нет корней
Автор ответа:
1
Ответ:
№ 1-2 см на фото
Пошаговое объяснение:
3) непонятно, второй и третий логарифмы стоят в степени числа 5 или нет?
4) Т.к. логарифмы равны, основания логарифмов равны, то равны и выражения, стоящие под логарифмом
х-7=х
х-х=7
0=7 -неверно, значит, решений нет
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: адимрфшь1
Предмет: Українська мова,
автор: ЖеняКаспрук
Предмет: Другие предметы,
автор: Диана1122
Предмет: Музыка,
автор: artt7890
Предмет: Математика,
автор: ДИМАШ228666