Question

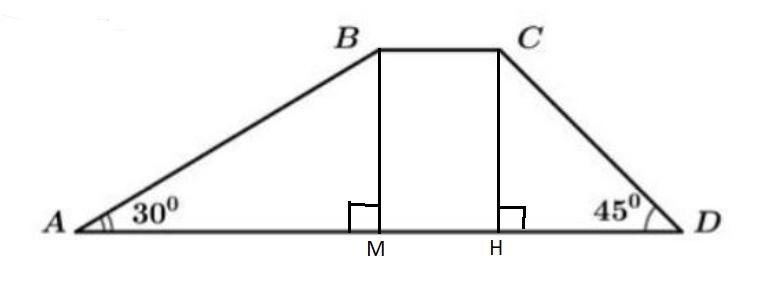
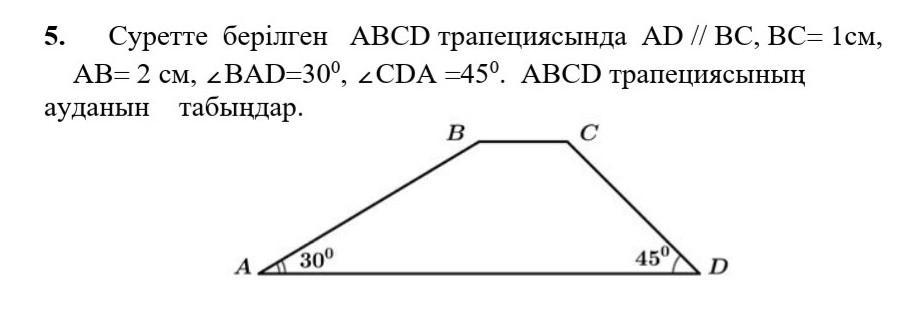
В трапеции ABCD, показанной на рисунке AD // BC, BC = 1 см, AB = 2 см, ∠BAD = 30 °, ∠CDA = 45 °. Найдите площадь трапеции ABCD​

Answer 1

Ответ:

Площадь трапеции равна $\dfrac{\sqrt{3} +3}{2}$ см²

Объяснение:

Пусть дана трапеция  ABCD , ВС= 1 см, АВ= 2 см.

∠ ВАD =30°, ∠СDА =45°.

Проведем высоты трапеции ВМ и СН

Рассмотрим Δ АВМ - прямоугольный.

По свойству катета, лежащего напротив угла в 30 ° , катет ВМ равен половине гипотенузы АВ.

Значит, ВМ= 1 см.

Найдем катет АМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов $AM^{2} =AB^{2} -BM^{2} ;\\AM=\sqrt{AB^{2} -BM^{2} } ;\\AM= \sqrt{2^{2} -1^{2} } =\sqrt{4-1} =\sqrt{3}$

$AM=\sqrt{3}$ см.

Отрезки ВМ и СН равны, как отрезки, заключенные между параллельными прямыми.

СН=ВМ = 1 см.

Рассмотрим Δ CHD - прямоугольный, так как ∠СDА =45°,

то ∠DCH=90°-45°=45°.

Тогда треугольник равнобедренный, если в нем два угла равны.

СН=НD=1 cм

Найдем длину большего основания

AD= AM+MH+HD;

$AD= \sqrt{3} +1+1=\sqrt{3} +2$ см.

Найдем площадь трапеции по формуле

$S= \dfrac{a+b}{a} \cdot h,$

где  a,b - основания трапеции,  h - высота трапеции.

$S= \dfrac{AD+BC}{2} \cdot BM ;\\\\S= \dfrac{\sqrt{3}+2+1 }{2} \cdot 1=\dfrac{\sqrt{3} +3}{2} \cdot1=\dfrac{\sqrt{3} +3}{2}$

Значит, площадь трапеции равна $\dfrac{\sqrt{3} +3}{2}$ см²