Question

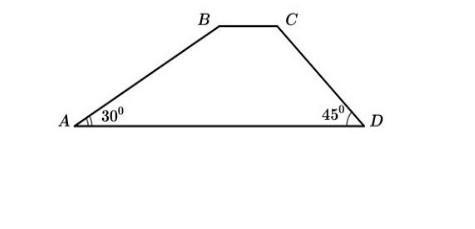
В трапеции ABCD, показанной на рисунке AD // BC, BC = 2 см, AB = 4 см, ∠BAD = 30 °, ∠CDA = 45 °. Найдите площадь трапеции ABCD​

Answer 1

Ответ: 2√3+6 см²

Объяснение:  

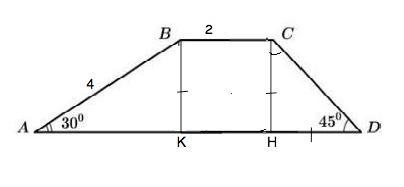
   Опустим перпендикуляры ВК и СН на сторону АD. Они проведены между параллельными прямыми и поэтому равны.

   По одной из формул площади трапеции Ѕ(АВСD)=ВК•(ВС+АD):2.

В ⊿ АВК катет ВК противолежит углу 30°.  ⇒ ВК=АВ:2=2 (см) по свойству такого угла.

В ⊿ СНD из суммы углов треугольника ∠ HCD равен 45° ⇒ DH=CH=BK=2 см.

AK=AB•cos30°=2√3 ( или по т.Пифагора).

☐КВСН - прямоугольник, КН=ВС=2 см⇒

AD=AK+KH+HD=2√3+2+2 см

S(ABCD)=2•(2√3+4+2):2=2√3+6 см²