Question

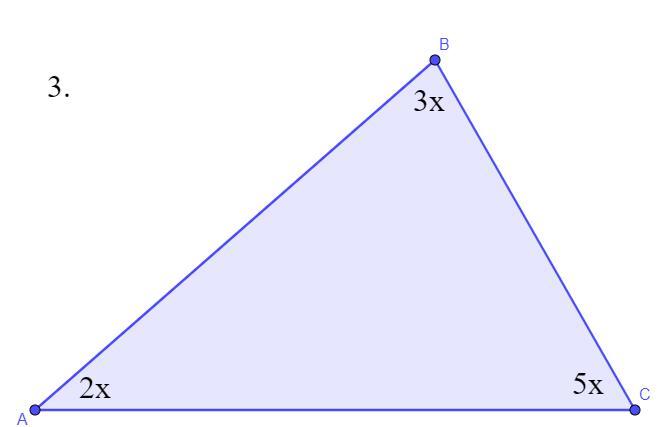
3. Найдите углы треугольника АВС, если <А: <В : <С = 2:3:5.

a) Определите вид треугольника АВС.

b) Укажите самую длинную сторону треугольника, обоснуйте свой ответ.

​

Answer 1

Ответ:

3.

∠A = 36°

∠B = 54°

∠C = 90°

4.

AB = BC = 8,3 см

AC = 3,5 см

Объяснение:

3.

Дано: ∠A : ∠B : ∠C = 2 : 3 : 5

Найти: ∠A,∠B,∠C - ?

Найти: Наибольшую сторону треугольника ΔABC

Решение:

Введем коэффициент пропорциональности x, тогда по условию задачи угол ∠A = 2x, ∠B = 3x, ∠C = 5x.

По теореме про сумму углов треугольника (ΔABC):

∠A + ∠B + ∠C = 180°

2x + 3x + 5x = 180°

10x = 180°|:10

x = 18°

∠A = 2x = 2 * 18° = 36°.

∠B = 3x = 3 * 18° = 54°.

∠C = 5x = 5 * 18° = 90°.

По теореме против наибольшего угла лежит наибольшая сторона, так как в треугольнике ΔABC угол ∠C = 90° - наибольший, то сторона треугольника, которая лежит против этого угла, то есть

сторона AB - наибольшая.

4.

По определению равнобедренного треугольника две его стороны равны (боковые стороны), а третья сторона называется основание.

Так как неизвестно какая длинна у боковой стороны, а какая у основания, то следует рассматривать два случая при решении данной задачи, чтобы проверить существует ли треугольник с данными сторонами.

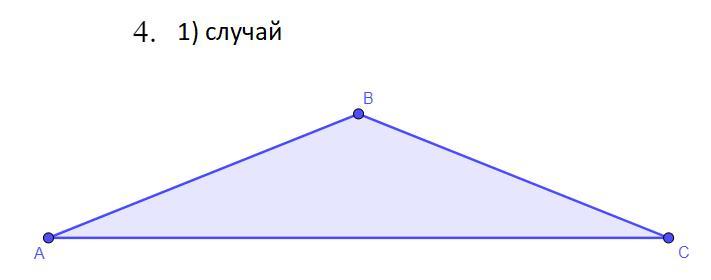
1) случай

Дано: AB = BC = 3,5 см, AC = 8,3 см

Доказать: существование ΔABC

Решение:

Запишем неравенство треугольника для треугольника ΔABC:

$\left \{\begin{array}{l} AB < AC + CB \\ AC < AB + BC \\ BC < BA + AC\end{array} \right$  $\left \{\begin{array}{l} 3,5 < 8,3 + 3,5 \\ 8,3 < 3,5 + 3,5 \\ 3,5 < 3,5 +8,3 \end{array} \right$  $\left \{\begin{array}{l} 3,5 < 11,8 \\ 8,3 < 7 \\ 3,5 < 11,8 \end{array} \right$

Утверждение $\boxed{8,3 < 7}$ - неверное, следовательно неравенство треугольника не выполняется и треугольник не существует.

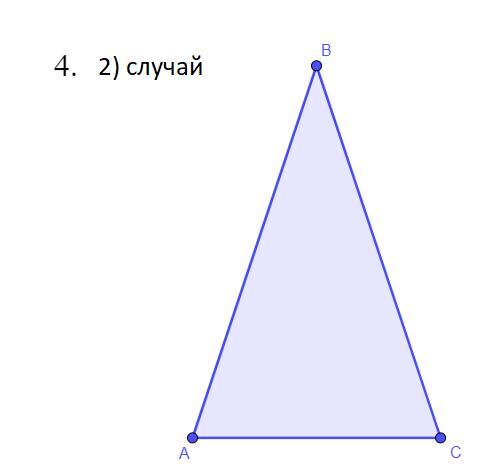
2) случай

Дано: AB = BC = 8,3 см, AC = 3,5 см

Доказать: существование ΔABC

Решение:

Запишем неравенство треугольника для треугольника ΔABC:

$\left \{\begin{array}{l} AB < AC + CB \\ AC < AB + BC \\ BC < BA + AC\end{array} \right$  $\left \{\begin{array}{l} 8,3 < 3,5 + 8,3 \\ 3,5 < 8,3 + 8,3 \\ 8,3 < 3,5 + 8,3\end{array} \right$  $\left \{\begin{array}{l} 8,3 < 11,8 \\ 3,5 < 16,6 \\ 8,3 < 11,8\end{array} \right$  

Все неравенства выполняются, следовательно треугольник существует.

---------------------------------------------------------------------------------------------------------

Таким образом, боковые стороны треугольника равны 8,3 см, а основание - 3,5 см.

То есть:

AB = BC = 8,3 см

AC = 3,5 см