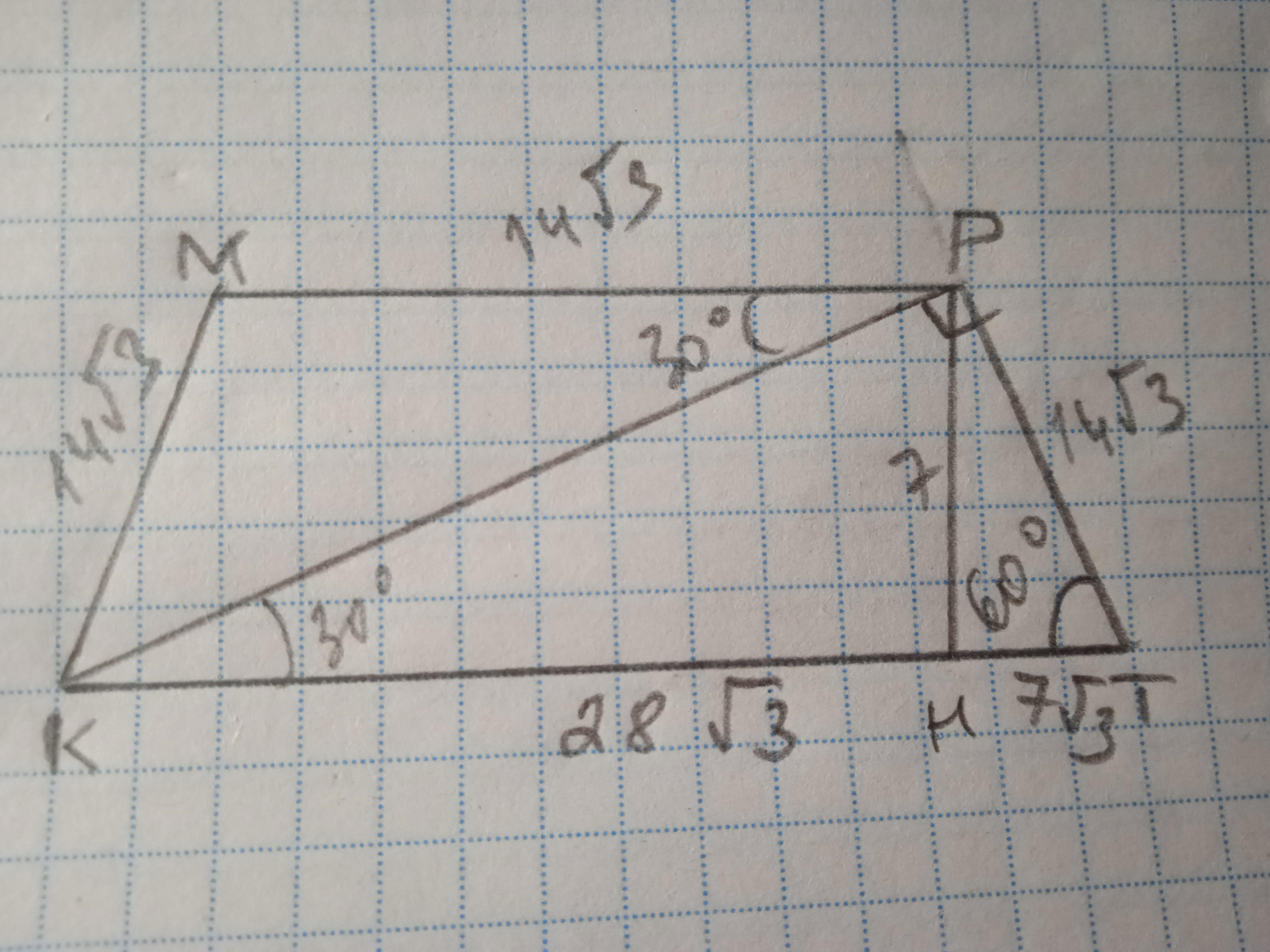
в равнобедренной трапеции диагональ перпендикулярна боковой стороне найдите площадь трапеции если большее основание равно 28√3дм найдите площадь данной трапеции
СРОЧНО
Ответы
В равнобедренной трапеции диагональ перпендикулярна боковой стороне, а один из углов равен 60°. Найдите площадь трапеции если большее основание равно 28√3 дм.
Ответ:
147√3 дм²
Объяснение:
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°, КР⊥РТ; КТ=28√3 дм. Найти S(КМРТ).
Рассмотрим ΔКРТ - прямоугольный; ∠РКТ=90-60=30°, значит, РТ=0,5КТ=6√3 дмпо свойству катета, лежащего против угла 30 градусов.
Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;
∠ТРН=90-60=30°, значит, ТН=0,5РТ=7√3 дм.
Найдем РН по теореме Пифагора:
РН²=РТ²-ТН²=196-147=49; РН=7 дм.
Найдем МР. ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР; ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=14√3 дм.
S(КМРТ)=(МР+КТ)/2 * РН = (14√3+28√3)/2 * 7=(21√3)*7=147√3 дм²