Предмет: Алгебра,
автор: Аноним
Помогите решить, алгебра 10 класс
Очень срочно
Приложения:
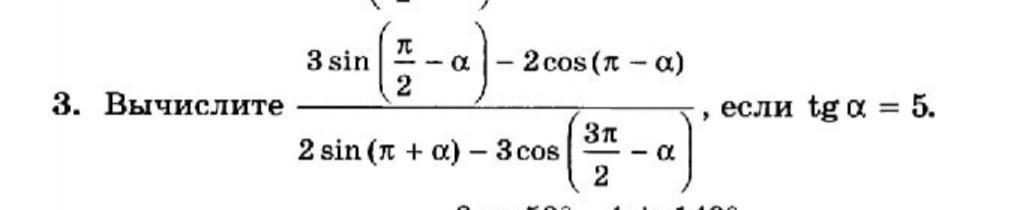
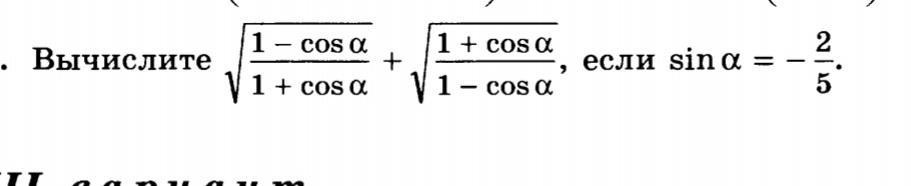
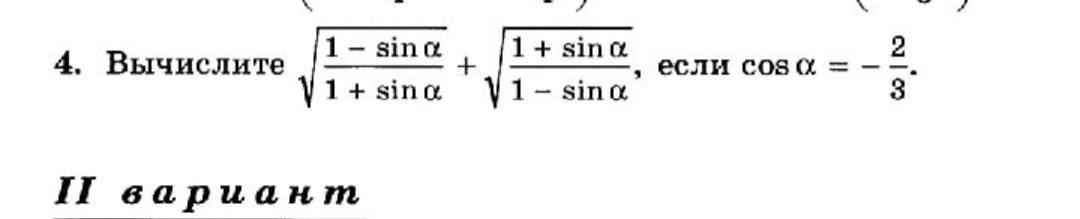
Ответы
Автор ответа:
1
3.
4.
5.
аналогично предыдущему заданию
Похожие вопросы
Предмет: Английский язык,
автор: bushuevaai1999
Предмет: Русский язык,
автор: safonowamarija
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Диана0711