Предмет: Геометрия,
автор: bilesolej4716
помогите как это правильнт решать
Приложения:
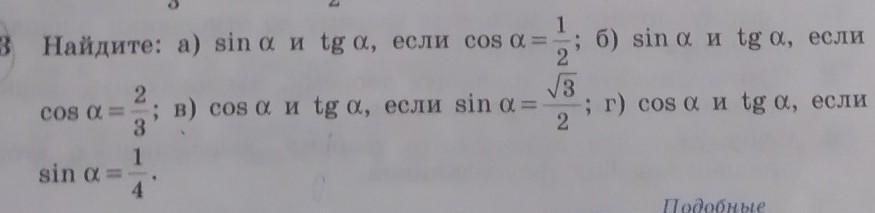
Ответы
Автор ответа:
0
Ответ:
Углы не указаны, поэтому предположим, что а в первой четверти.
а)
б)
в)
из пункта а)
г)
Похожие вопросы
Предмет: Русский язык,
автор: COJIHLje
Предмет: Русский язык,
автор: Алина240502
Предмет: Українська мова,
автор: liptuga2013
Предмет: Окружающий мир,
автор: ALYALI61