Предмет: Геометрия,
автор: nastya31200113
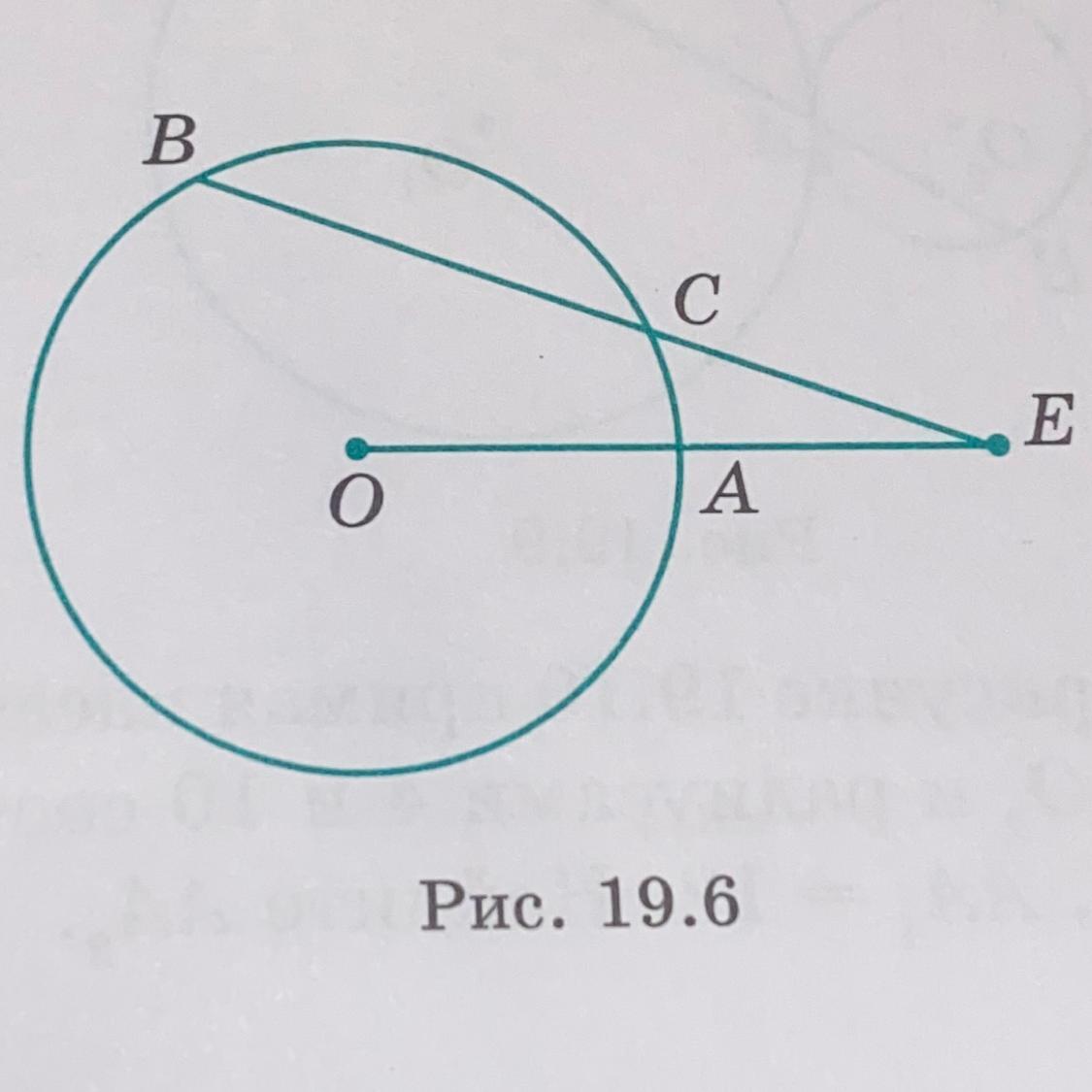
9. Радиус окружности равен 4 см. На продолжении радиуса взята точка Е, отстоящая от центра О окружности на расстояние 8 см. Через точку Е проведён луч, пересекающий окружность в точках В и С (рис. 19.6), BE = 10. Найдите СЕ.
Приложения:
Ответы
Автор ответа:
5
Ответ:
см
Объяснение:
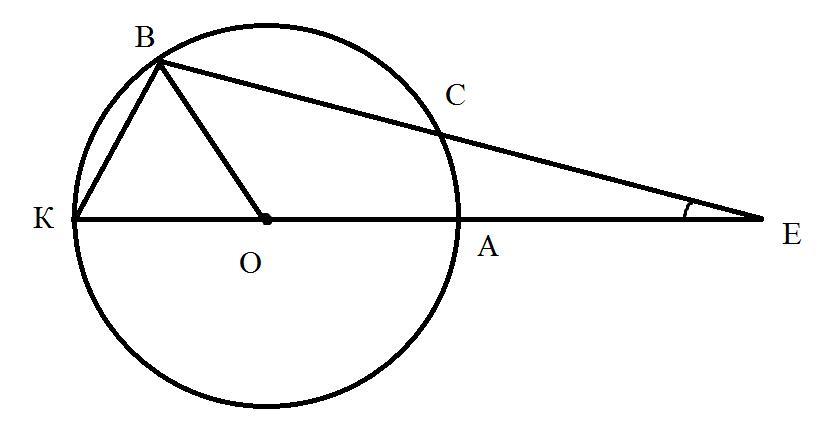
Продолжим ОЕ до ЕК, где АК - диаметр окружности.
Заметим, что ЕК=ОЕ+ОК=8+4 (так как радиус окружности)=12 см.
ΔВКЕ≅ΔСАЕ по 1-му признаку подобия. ∠Е - общий, - так как это секущие окружности, проведенные из одной точки.
Теперь в это соотношение подставим известные данные.
Умножим обе части на 10, получим
см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Oxana9676
Предмет: Русский язык,
автор: fhdfvbc
Предмет: Окружающий мир,
автор: myrzik301984
Предмет: Геометрия,
автор: Шелкунчик228
Предмет: Математика,
автор: Амир0102