Предмет: Геометрия,
автор: hhhhhhhhh4
Найдите периметр треугольника с площадью 20√3см²и углом 60 градусов, если стороны прямолежащие к данному углу, относятся как 4:5
Ответы
Автор ответа:
2
Ответ:
По теореме косинусов найдем третью сторону:
Приложения:
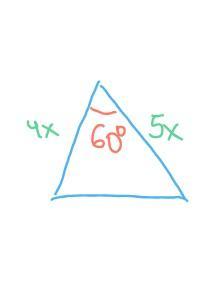
Похожие вопросы
Предмет: Русский язык,
автор: yulka1105
Предмет: Русский язык,
автор: незнайка93
Предмет: Русский язык,
автор: Перс1
Предмет: Математика,
автор: VatikanikLusik33