Сопоставьте функции и графики функции Количество связей:
Ответы
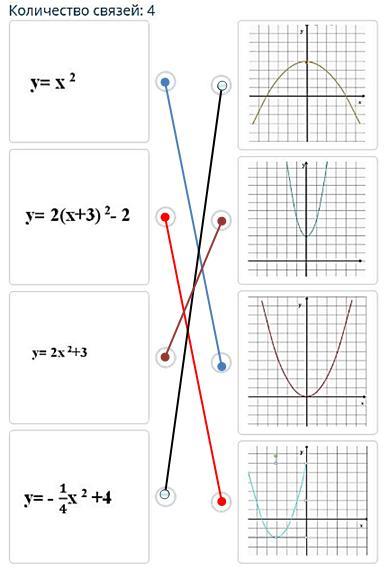
Пусть для определенности: функции имею номера 1, 2, 3 и 4, а графики - а, б, в и г.
1. у = х² - гоафик красного цвета - в), т.к. ветви параболы направлены вверх и проходит через начало координат.
2. у = 2(х + 3)² - 2 - этот график можно получить из графика функции у = х² "сузив" его в 2 раза вдоль оси Оу и смещением его на 3 единицы влево вдоль оси Ох и на 2 едини цы вниз вдолль оси Оу, т.е. ее график - это г (голубого цвета).
3. у = 2х² + 3 - этот график можно получить из графика функции у = х² "сузив" его в 2 раза вдоль оси Оу и смещением его на 3 единицы вверх вдоль оси Оу, т.е. ее график - это б (синего цвета).
4. у = -1/4 · х² + 4 - ветви этой параболы направлены вниз (-1/4 < 0), график ее можно получить, отразив график функции у = х² относительно оси Ох (получим график функции у = -х²), "растянув" в 4 раза график функции у = -х² вдоль оси Ох и сдвинув его на 4 единицы вверх вдоль оси Оу, т.е. ее график -это а (коричневого цвета).
Ответ:
Сопоставление графиков и формул в приложении.
Графики, соответствующие уравнениям параболы легко определить по абсциссе вершины и направлению ветвь:
Если уравнение параболы задаётся в виде y = a·(x-x₀)²+y₀,то абсцисса вершины x=x₀ и при a>0 ветви направлены вверх, а при a<0 ветви направлены вниз.
Тогда:
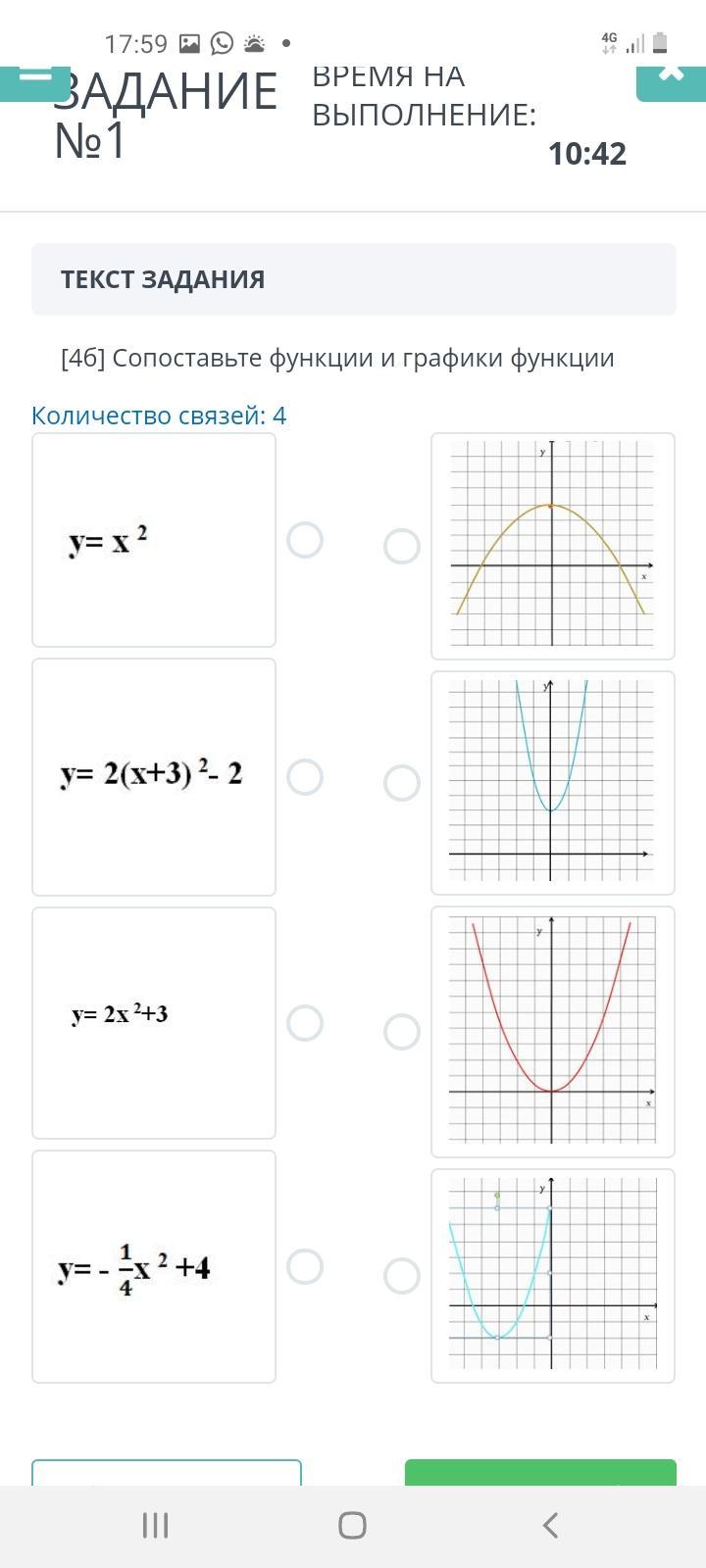
y = x² - ветви направлены вверх и абсцисса вершины x=0;
y = 2·(x+3)²-2 - ветви направлены вверх и абсцисса вершины x= -3;
y = 2·x²+3 - ветви направлены вверх и абсцисса вершины x=0;
y = (-1/4)·x²+4 - ветви направлены вниз и абсцисса вершины x=0.