Question

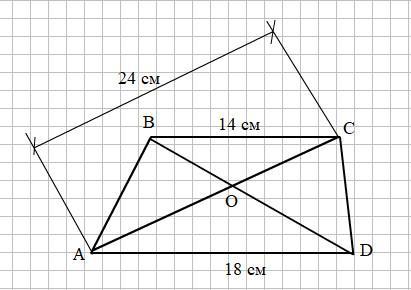
в трапеции ABCD известно,что AD=18см, ВС=14 см, АС=24см. Найдите отрезки на которые диагональ АС делится точкой пересечения диагоналей 

Answer 1

О-точка пересечения диагоналей. Треугольники BОС и DOA подобны по трем равным углам⇒будет верна пропорция BC:AD=OC:AO
Пусть OC-x, AO-24-x
14/18=x/24-x
18*x=14*(24-x)
18x=336-14x
18x+14x=336
32x=336
x=336:32=10,5cм-OC
24-10,5=13,5см-АО

Answer 2

Ответ:

АО = 13,5 см;   СО = 10,5 см

Объяснение:

Смотри рисунок на прикреплённом фото.

Δ СОВ ~ Δ AOD по двум углам:

∠ВСО = ∠DAO как накрест лежащие при ВС║AD и секущей АС;

∠СВО = ∠АDO как накрест лежащие при ВС║AD и секущей BD.

Соответственные стороны подобных треугольников пропорциональны. Коэффициент пропорциональности k = BC/AD = 14/18 = 7/9.

CO/AO = k;   CO/(AC - CO) = k;

CO = k · (AC - CO)

CO = k · AC - k · CO

CO = k · AC/(1 + k) = 7/9 · 24/(1 + 7/9) = 21/2 = 10,5 (см)

АО = АС - СО = 24 - 10,5 = 13,5 (см)